NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals
NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals are an educational aid for students that help them solve and learn simple and difficult tasks. It includes complete set of questions organized with advanced level of difficulty, which provide students ample opportunity to apply combination and skills. Get free NCERT Solutions for Class 9 Maths, Chapter 8 Quadrilaterals. NCERT Solutions will help the students to understand the concept of Quadrilaterals mainly basics, properties and some important theorems. These solutions can not only help students to clear their doubts but also to prepare more efficiently.Chapter 8 – Quadrilaterals
Download NCERT Solutions for Class 9 Maths Chapter 8 – Quadrilaterals















Access Answers to NCERT Class 9 Maths Chapter 8 – Quadrilaterals
Exercise 8.1 Page: 146
1. The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.
Solution:
Let the common ratio between the angles be = x.
We know that the sum of the interior angles of the quadrilateral = 360°
Now,
3x+5x+9x+13x = 360°
⇒ 30x = 360°
⇒ x = 12°
, Angles of the quadrilateral are:
3x = 3×12° = 36°
5x = 5×12° = 60°
9x = 9×12° = 108°
13x = 13×12° = 156°
2. If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Solution:
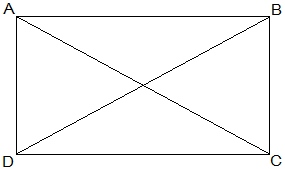
Given that,
AC = BD
To show that, ABCD is a rectangle if the diagonals of a parallelogram are equal
To show ABCD is a rectangle we have to prove that one of its interior angles is right angled.
Proof,
In ΔABC and ΔBAD,
AB = BA (Common)
BC = AD (Opposite sides of a parallelogram are equal)
AC = BD (Given)
Therefore, ΔABC ≅ ΔBAD [SSS congruency]
∠A = ∠B [Corresponding parts of Congruent Triangles]
also,
∠A+∠B = 180° (Sum of the angles on the same side of the transversal)
⇒ 2∠A = 180°
⇒ ∠A = 90° = ∠B
Therefore, ABCD is a rectangle.
Hence Proved.
3. Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Solution:
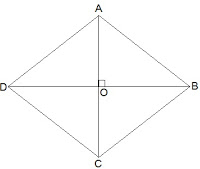
Let ABCD be a quadrilateral whose diagonals bisect each other at right angles.
Given that,
OA = OC
OB = OD
and ∠AOB = ∠BOC = ∠OCD = ∠ODA = 90°
To show that,
if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
i.e., we have to prove that ABCD is parallelogram and AB = BC = CD = AD
Proof,
In ΔAOB and ΔCOB,
OA = OC (Given)
∠AOB = ∠COB (Opposite sides of a parallelogram are equal)
OB = OB (Common)
Therefore, ΔAOB ≅ ΔCOB [SAS congruency]
Thus, AB = BC [CPCT]
Similarly we can prove,
BC = CD
CD = AD
AD = AB
, AB = BC = CD = AD
Opposites sides of a quadrilateral are equal hence ABCD is a parallelogram.
, ABCD is rhombus as it is a parallelogram whose diagonals intersect at right angle.
Hence Proved.
4. Show that the diagonals of a square are equal and bisect each other at right angles.
Solution:
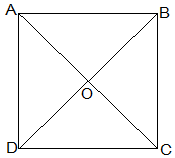
Let ABCD be a square and its diagonals AC and BD intersect each other at O.
To show that,
AC = BD
AO = OC
and ∠AOB = 90°
Proof,
In ΔABC and ΔBAD,
AB = BA (Common)
∠ABC = ∠BAD = 90°
BC = AD (Given)
ΔABC ≅ ΔBAD [SAS congruency]
Thus,
AC = BD [CPCT]
diagonals are equal.
Now,
In ΔAOB and ΔCOD,
∠BAO = ∠DCO (Alternate interior angles)
∠AOB = ∠COD (Vertically opposite)
AB = CD (Given)
, ΔAOB ≅ ΔCOD [AAS congruency]
Thus,
AO = CO [CPCT].
, Diagonal bisect each other.
Now,
In ΔAOB and ΔCOB,
OB = OB (Given)
AO = CO (diagonals are bisected)
AB = CB (Sides of the square)
, ΔAOB ≅ ΔCOB [SSS congruency]
also, ∠AOB = ∠COB
∠AOB+∠COB = 180° (Linear pair)
Thus, ∠AOB = ∠COB = 90°
, Diagonals bisect each other at right angles
5. Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Solution:
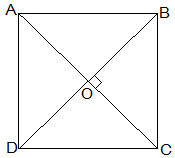
Given that,
Let ABCD be a quadrilateral and its diagonals AC and BD bisect each other at right angle at O.
To prove that,
The Quadrilateral ABCD is a square.
Proof,
In ΔAOB and ΔCOD,
AO = CO (Diagonals bisect each other)
∠AOB = ∠COD (Vertically opposite)
OB = OD (Diagonals bisect each other)
, ΔAOB ≅ ΔCOD [SAS congruency]
Thus,
AB = CD [CPCT] — (i)
also,
∠OAB = ∠OCD (Alternate interior angles)
⇒ AB || CD
Now,
In ΔAOD and ΔCOD,
AO = CO (Diagonals bisect each other)
∠AOD = ∠COD (Vertically opposite)
OD = OD (Common)
, ΔAOD ≅ ΔCOD [SAS congruency]
Thus,
AD = CD [CPCT] — (ii)
also,
AD = BC and AD = CD
⇒ AD = BC = CD = AB — (ii)
also, ∠ADC = ∠BCD [CPCT]
and ∠ADC+∠BCD = 180° (co-interior angles)
⇒ 2∠ADC = 180°
⇒∠ADC = 90° — (iii)
One of the interior angles is right angle.
Thus, from (i), (ii) and (iii) given quadrilateral ABCD is a square.
Hence Proved.
6. Diagonal AC of a parallelogram ABCD bisects ∠A (see Fig. 8.19). Show that
(i) it bisects ∠C also,
(ii) ABCD is a rhombus.
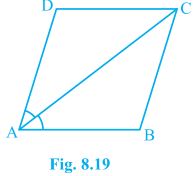
Solution:
(i) In ΔADC and ΔCBA,
AD = CB (Opposite sides of a parallelogram)
DC = BA (Opposite sides of a parallelogram)
AC = CA (Common Side)
, ΔADC ≅ ΔCBA [SSS congruency]
Thus,
∠ACD = ∠CAB by CPCT
and ∠CAB = ∠CAD (Given)
⇒ ∠ACD = ∠BCA
Thus,
AC bisects ∠C also.
(ii) ∠ACD = ∠CAD (Proved above)
⇒ AD = CD (Opposite sides of equal angles of a triangle are equal)
Also, AB = BC = CD = DA (Opposite sides of a parallelogram)
Thus,
ABCD is a rhombus.
7. ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
Solution:
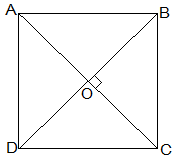
Given that,
ABCD is a rhombus.
AC and BD are its diagonals.
Proof,
AD = CD (Sides of a rhombus)
∠DAC = ∠DCA (Angles opposite of equal sides of a triangle are equal.)
also, AB || CD
⇒∠DAC = ∠BCA (Alternate interior angles)
⇒∠DCA = ∠BCA
, AC bisects ∠C.
Similarly,
We can prove that diagonal AC bisects ∠A.
Following the same method,
We can prove that the diagonal BD bisects ∠B and ∠D.
8. ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
(i) ABCD is a square
(ii) Diagonal BD bisects ∠B as well as ∠D.
Solution:
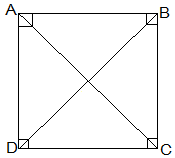
(i) ∠DAC = ∠DCA (AC bisects ∠A as well as ∠C)
⇒ AD = CD (Sides opposite to equal angles of a triangle are equal)
also, CD = AB (Opposite sides of a rectangle)
,AB = BC = CD = AD
Thus, ABCD is a square.
(ii) In ΔBCD,
BC = CD
⇒ ∠CDB = ∠CBD (Angles opposite to equal sides are equal)
also, ∠CDB = ∠ABD (Alternate interior angles)
⇒ ∠CBD = ∠ABD
Thus, BD bisects ∠B
Now,
∠CBD = ∠ADB
⇒ ∠CDB = ∠ADB
Thus, BD bisects ∠D
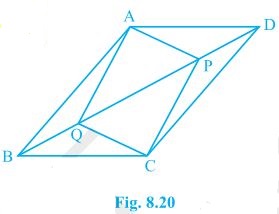
9. In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig. 8.20). Show that:
(i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
(v) APCQ is a parallelogram
Solution:
(i) In ΔAPD and ΔCQB,
DP = BQ (Given)
∠ADP = ∠CBQ (Alternate interior angles)
AD = BC (Opposite sides of a parallelogram)
Thus, ΔAPD ≅ ΔCQB [SAS congruency]
(ii) AP = CQ by CPCT as ΔAPD ≅ ΔCQB.
(iii) In ΔAQB and ΔCPD,
BQ = DP (Given)
∠ABQ = ∠CDP (Alternate interior angles)
AB = CD (Opposite sides of a parallelogram)
Thus, ΔAQB ≅ ΔCPD [SAS congruency]
(iv) As ΔAQB ≅ ΔCPD
AQ = CP [CPCT]
(v) From the questions (ii) and (iv), it is clear that APCQ has equal opposite sides and also has equal and opposite angles. , APCQ is a parallelogram.
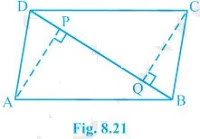
10. ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see Fig. 8.21). Show that
(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ
Solution:
(i) In ΔAPB and ΔCQD,
∠ABP = ∠CDQ (Alternate interior angles)
∠APB = ∠CQD (= 90o as AP and CQ are perpendiculars)
AB = CD (ABCD is a parallelogram)
, ΔAPB ≅ ΔCQD [AAS congruency]
(ii) As ΔAPB ≅ ΔCQD.
, AP = CQ [CPCT]
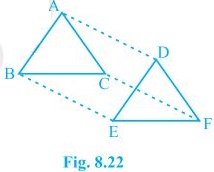
11. In ΔABC and ΔDEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively (see Fig. 8.22).
Show that
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ΔABC ≅ ΔDEF.
Solution:
(i) AB = DE and AB || DE (Given)
Two opposite sides of a quadrilateral are equal and parallel to each other.
Thus, quadrilateral ABED is a parallelogram
(ii) Again BC = EF and BC || EF.
Thus, quadrilateral BEFC is a parallelogram.
(iii) Since ABED and BEFC are parallelograms.
⇒ AD = BE and BE = CF (Opposite sides of a parallelogram are equal)
, AD = CF.
Also, AD || BE and BE || CF (Opposite sides of a parallelogram are parallel)
, AD || CF
(iv) AD and CF are opposite sides of quadrilateral ACFD which are equal and parallel to each other. Thus, it is a parallelogram.
(v) Since ACFD is a parallelogram
AC || DF and AC = DF
(vi) In ΔABC and ΔDEF,
AB = DE (Given)
BC = EF (Given)
AC = DF (Opposite sides of a parallelogram)
, ΔABC ≅ ΔDEF [SSS congruency]
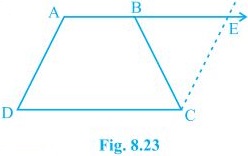
12. ABCD is a trapezium in which AB || CD and AD = BC (see Fig. 8.23). Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ΔABC ≅ ΔBAD
(iv) diagonal AC = diagonal BD
[Hint : Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
Solution:
To Construct: Draw a line through C parallel to DA intersecting AB produced at E.
(i) CE = AD (Opposite sides of a parallelogram)
AD = BC (Given)
, BC = CE
⇒∠CBE = ∠CEB
also,
∠A+∠CBE = 180° (Angles on the same side of transversal and ∠CBE = ∠CEB)
∠B +∠CBE = 180° ( As Linear pair)
⇒∠A = ∠B
(ii) ∠A+∠D = ∠B+∠C = 180° (Angles on the same side of transversal)
⇒∠A+∠D = ∠A+∠C (∠A = ∠B)
⇒∠D = ∠C
(iii) In ΔABC and ΔBAD,
AB = AB (Common)
∠DBA = ∠CBA
AD = BC (Given)
, ΔABC ≅ ΔBAD [SAS congruency]
(iv) Diagonal AC = diagonal BD by CPCT as ΔABC ≅ ΔBA.
Exercise 8.2 Page: 150
1. ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig 8.29). AC is a diagonal. Show that:
(i) SR || AC and SR = 1/2 AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
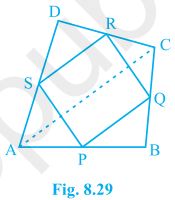
Solution:
(i) In ΔDAC,
R is the mid point of DC and S is the mid point of DA.
Thus by mid point theorem, SR || AC and SR = ½ AC
(ii) In ΔBAC,
P is the mid point of AB and Q is the mid point of BC.
Thus by mid point theorem, PQ || AC and PQ = ½ AC
also, SR = ½ AC
, PQ = SR
(iii) SR || AC ———————- from question (i)
and, PQ || AC ———————- from question (ii)
⇒ SR || PQ – from (i) and (ii)
also, PQ = SR
, PQRS is a parallelogram.
2. ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Solution:
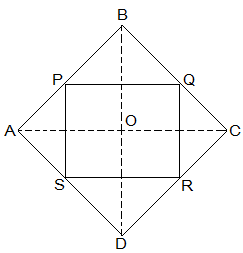
Given in the question,
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively.
To Prove,
PQRS is a rectangle.
Construction,
Join AC and BD.
Proof:
In ΔDRS and ΔBPQ,
DS = BQ (Halves of the opposite sides of the rhombus)
∠SDR = ∠QBP (Opposite angles of the rhombus)
DR = BP (Halves of the opposite sides of the rhombus)
, ΔDRS ≅ ΔBPQ [SAS congruency]
RS = PQ [CPCT]———————- (i)
In ΔQCR and ΔSAP,
RC = PA (Halves of the opposite sides of the rhombus)
∠RCQ = ∠PAS (Opposite angles of the rhombus)
CQ = AS (Halves of the opposite sides of the rhombus)
, ΔQCR ≅ ΔSAP [SAS congruency]
RQ = SP [CPCT]———————- (ii)
Now,
In ΔCDB,
R and Q are the mid points of CD and BC respectively.
⇒ QR || BD
also,
P and S are the mid points of AD and AB respectively.
⇒ PS || BD
⇒ QR || PS
, PQRS is a parallelogram.
also, ∠PQR = 90°
Now,
In PQRS,
RS = PQ and RQ = SP from (i) and (ii)
∠Q = 90°
, PQRS is a rectangle.
3. ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Solution:
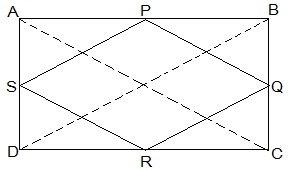
Given in the question,
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively.
Construction,
Join AC and BD.
To Prove,
PQRS is a rhombus.
Proof:
In ΔABC
P and Q are the mid-points of AB and BC respectively
, PQ || AC and PQ = ½ AC (Midpoint theorem) — (i)
In ΔADC,
SR || AC and SR = ½ AC (Midpoint theorem) — (ii)
So, PQ || SR and PQ = SR
As in quadrilateral PQRS one pair of opposite sides is equal and parallel to each other, so, it is a parallelogram.
, PS || QR and PS = QR (Opposite sides of parallelogram) — (iii)
Now,
In ΔBCD,
Q and R are mid points of side BC and CD respectively.
, QR || BD and QR = ½ BD (Midpoint theorem) — (iv)
AC = BD (Diagonals of a rectangle are equal) — (v)
From equations (i), (ii), (iii), (iv) and (v),
PQ = QR = SR = PS
So, PQRS is a rhombus.
Hence Proved
4. ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.
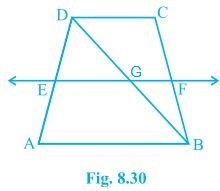
Solution:
Given that,
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD.
To prove,
F is the mid-point of BC.
Proof,
BD intersected EF at G.
In ΔBAD,
E is the mid point of AD and also EG || AB.
Thus, G is the mid point of BD (Converse of mid point theorem)
Now,
In ΔBDC,
G is the mid point of BD and also GF || AB || DC.
Thus, F is the mid point of BC (Converse of mid point theorem)
5. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see Fig. 8.31). Show that the line segments AF and EC trisect the diagonal BD.
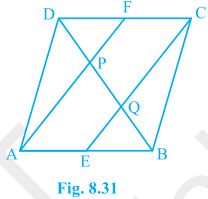
Solution:
Given that,
ABCD is a parallelogram. E and F are the mid-points of sides AB and CD respectively.
To show,
AF and EC trisect the diagonal BD.
Proof,
ABCD is a parallelogram
, AB || CD
also, AE || FC
Now,
AB = CD (Opposite sides of parallelogram ABCD)
⇒½ AB = ½ CD
⇒ AE = FC (E and F are midpoints of side AB and CD)
AECF is a parallelogram (AE and CF are parallel and equal to each other)
AF || EC (Opposite sides of a parallelogram)
Now,
In ΔDQC,
F is mid point of side DC and FP || CQ (as AF || EC).
P is the mid-point of DQ (Converse of mid-point theorem)
⇒ DP = PQ — (i)
Similarly,
In ΔAPB,
E is midpoint of side AB and EQ || AP (as AF || EC).
Q is the mid-point of PB (Converse of mid-point theorem)
⇒ PQ = QB — (ii)
From equations (i) and (i),
DP = PQ = BQ
Hence, the line segments AF and EC trisect the diagonal BD.
Hence Proved.
6. Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Solution:
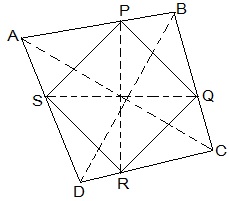
Let ABCD be a quadrilateral and P, Q, R and S are the mid points of AB, BC, CD and DA respectively.
Now,
In ΔACD,
R and S are the mid points of CD and DA respectively.
, SR || AC.
Similarly we can show that,
PQ || AC,
PS || BD and
QR || BD
, PQRS is parallelogram.
PR and QS are the diagonals of the parallelogram PQRS. So, they will bisect each other.
7. ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = ½ AB
Solution:
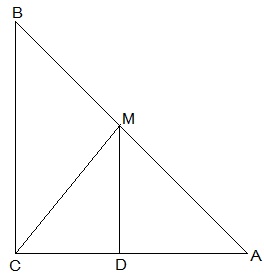
(i) In ΔACB,
M is the midpoint of AB and MD || BC
, D is the midpoint of AC (Converse of mid point theorem)
(ii) ∠ACB = ∠ADM (Corresponding angles)
also, ∠ACB = 90°
, ∠ADM = 90° and MD ⊥ AC
(iii) In ΔAMD and ΔCMD,
AD = CD (D is the midpoint of side AC)
∠ADM = ∠CDM (Each 90°)
DM = DM (common)
, ΔAMD ≅ ΔCMD [SAS congruency]
AM = CM [CPCT]
also, AM = ½ AB (M is midpoint of AB)
Hence, CM = MA = ½ AB
NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals
NCERT Solutions for Class 9 Maths Chapter 8 explains Angle Sum Property of a Quadrilateral, Types of Quadrilaterals and Mid-Point theorem.
Topics covered under this chapter help the students to understand the basics of a geometrical figure named as a quadrilateral, its properties and various important theorems. This chapter of NCERT Solutions for Class 9 Maths is extremely crucial as the formulas and theorem results are extensively used in several other maths concepts in higher grades.
Chapter 8-Quadrilaterals is a part of Unit IV, Geometry, and holds 28 marks of weightage in the final exam. Two or three questions are asked every year in the final examination from this chapter.
NCERT Solutions For Class 9 Maths Chapter 8 Exercises:
Get detailed solutions for all the questions listed under the below exercises:
Exercise 8.1 Solutions (12 Questions)
Exercise 8.2 Solutions(7 Questions) NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals NCERT Solutions for Class 9 Maths Chapter 8 is about Theorems and properties on Quadrilaterals. They are accompanied with explanatory figures and solved examples, which are explained in a comprehensive way. The main topics covered in this chapter include:
| Exercise | Topic |
| 8.1 | Introduction |
| 8.2 | Angle Sum Property of a Quadrilateral |
| 8.3 | Types of Quadrilaterals |
| 8.4 | Properties of a Parallelogram |
| 8.5 | Another Condition for a Quadrilateral to be a Parallelogram |
| 8.6 | The Mid-point Theorem |
| 8.7 | Summary |
Key Features of NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals
- NCERT solutions have been prepared in a logical and simple language.
- Pictorial presentation of all the questions.
- Emphasizes that learning should be activity-based and knowledge-driven.
- The solutions are explained in a well-organised way.
- Step by step approach used to solve all NCERT questions.
Frequently Asked Questions on NCERT Solutions for Class 9 Maths Chapter 8
What are the main topics covered in NCERT Solutions for Class 9 Maths Chapter 8?
The main topics covered in NCERT Solutions for Class 9 Maths Chapter 8 are given below:
8.1 Introduction of quadrilaterals
8.2 Angle Sum Property of a Quadrilateral
8.3 Types of Quadrilaterals
8.4 Properties of a Parallelogram
8.5 Another Condition for a Quadrilateral to be a Parallelogram
8.6 The Mid-point Theorem
8.7 Summary
How many questions are there in NCERT Solutions for Class 9 Maths Chapter 8?
NCERT Solutions for Class 9 Maths Chapter 8 contains two exercises. The first exercise has 12 questions and second exercise has 7 questions. Practising these exercises help you in scoring high in board exams and also help to ease the subject. These solutions are explained by subject matter experts to help you in clearing all the doubts.
What is the meaning of quadrilaterals according to NCERT Solutions for Class 9 Maths Chapter 8?
According to NCERT Solutions for Class 9 Maths Chapter 8 quadrilateral is a plane figure that has four sides or edges, and also has four corners or vertices. Quadrilaterals will typically be of standard shapes with four sides like rectangle, square, trapezoid, and kite or irregular and uncharacterized shapes.