NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles
NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles are given here. Students can either practise online or download these NCERT Solutions and practise different types of questions related to this chapter and thereby achieve maximum marks in their examinations. The relation of two objects being congruent is called congruence.
Chapter 7 – Congruence of Triangles contains 2 exercises. Subject experts prepare these NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles carefully, without any mistakes. Let us have a look at some of the concepts discussed in this chapter.
- Congruence of Plane Figures
- Congruence Among Line Segments
- Congruence of Angles
- Congruence of Triangles
- Criteria For Congruence of Triangles
- Congruence Among Right-Angled Triangles
Download the PDF of NCERT Solutions For Class 7 Maths Chapter 7 Congruence of Triangles









Access exercises of NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles
Access answers to Maths NCERT Solutions For Class 7 Chapter 7 – Congruence of Triangles
Exercise 7.1 Page: 137
1. Complete the following statements:
(a) Two line segments are congruent if ___________.
Solution:-
Two line segments are congruent if they have the same length.
(b) Among two congruent angles, one has a measure of 70o; the measure of the other angle is ___________.
Solution:-
Among two congruent angles, one has a measure of 70o; the measure of the other angle is 70o.
Because, if two angles have the same measure, they are congruent. Also, if two angles are congruent, their measure are same.
(c) When we write ∠A = ∠B, we actually mean .
Solution:-
When we write ∠A = ∠B, we actually mean m ∠A = m ∠B.
2. Give any two real-life examples for congruent shapes.
Solution:-
The two real-life example for congruent shapes are
(i) Fan feathers of same brand.
(ii) Size of chocolate in the same brand.
(iii) Size of pens in the same brand
3. If ΔABC ≅ ΔFED under the correspondence ABC ↔ FED, write all the corresponding congruent parts of the triangles.
Solution:-
Two triangles are congruent if pairs of corresponding sides and corresponding angles are equal.
All the corresponding congruent parts of the triangles are,
∠A ↔ ∠F, ∠B ↔ ∠E, ∠C ↔ ∠D
Correspondence between sides:

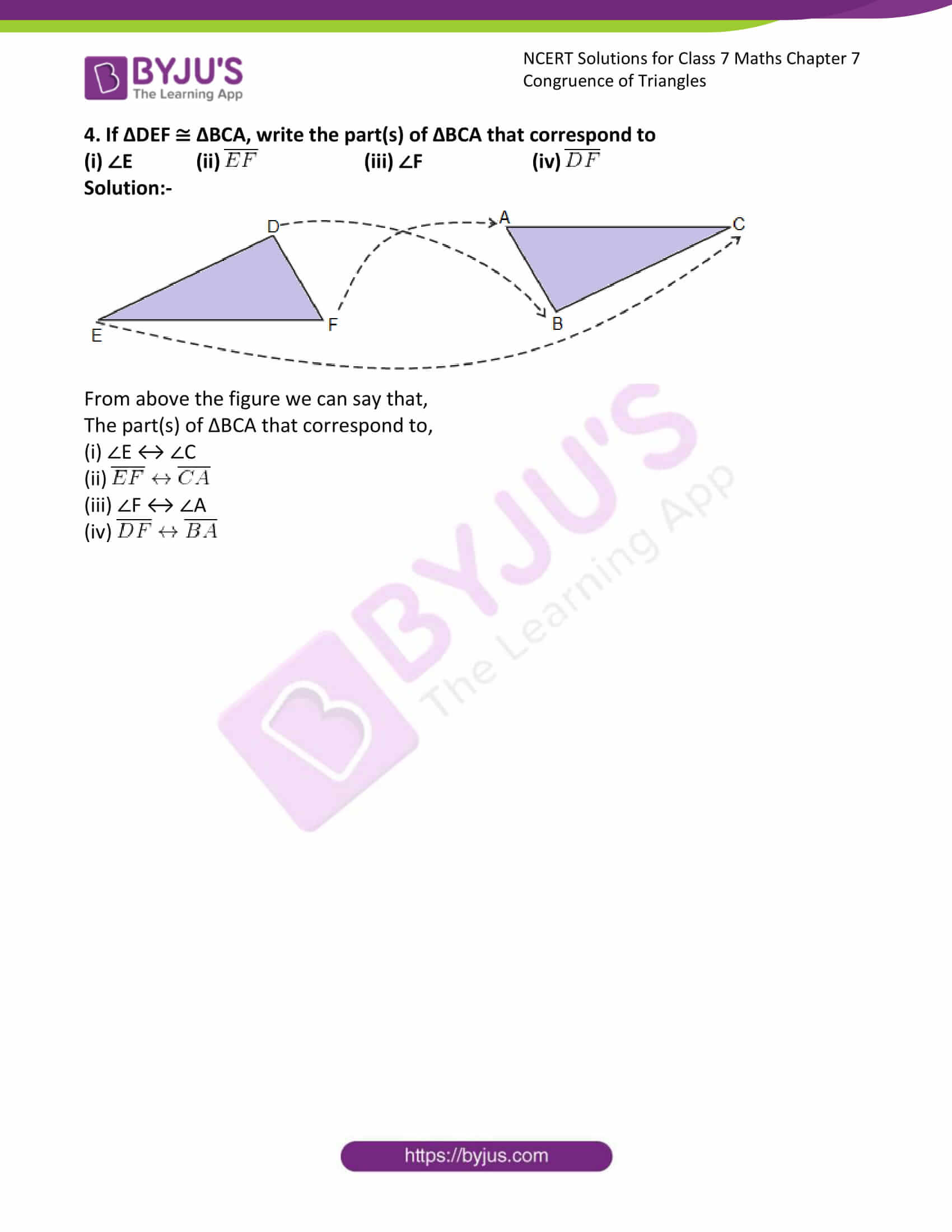
4. If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to
(i) ∠E (ii) (iii) ∠F (iv)
Solution:-

From above the figure we can say that,
The part(s) of ΔBCA that correspond to,
(i) ∠E ↔ ∠C
(ii)![]()
(iii) ∠F ↔ ∠A
(iv)![]()
Exercise 7.2 Page: 149
1. Which congruence criterion do you use in the following?
(a) Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF

Solution:-
By SSS congruence property:- Two triangles are congruent if the three sides of one triangle are respectively equal to the three sides of the other triangle.
ΔABC ≅ ΔDEF
(b) Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ

Solution:-
By SAS congruence property:- Two triangles are congruent if the two sides and the included angle of one are respectively equal to the two sides and the included angle of the other.
ΔACB ≅ ΔDEF
(c) Given: ∠MLN = ∠FGH
∠NML = ∠GFH
∠ML = ∠FG
So, ΔLMN ≅ ΔGFH

Solution:-
By ASA congruence property:- Two triangles are congruent if the two angles and the included side of one are respectively equal to the two angles and the included side of the other.
ΔLMN ≅ ΔGFH
(d) Given: EB = DB
AE = BC
∠A = ∠C = 90o
So, ΔABE ≅ ΔACD

Solution:-
By RHS congruence property:- Two right triangles are congruent if the hypotenuse and one side of the first triangle are respectively equal to the hypotenuse and one side of the second.
ΔABE ≅ ΔACD
2. You want to show that ΔART ≅ ΔPEN,
(a) If you have to use SSS criterion, then you need to show
(i) AR = (ii) RT = (iii) AT =

Solution:-
We know that,
SSS criterion is defined as, two triangles are congruent if the three sides of one triangle are respectively equal to the three sides of the other triangle.
∴ (i) AR = PE
(ii) RT = EN
(iii) AT = PN
(b) If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
(i) RT = and (ii) PN =

Solution:-
We know that,
SAS criterion is defined as, two triangles are congruent if the two sides and the included angle of one are respectively equal to the two sides and the included angle of the other.
∴ (i) RT = EN
(ii) PN = AT
(c) If it is given that AT = PN and you are to use ASA criterion, you need to have
(i) ? (ii) ?
Solution:-
We know that,
ASA criterion is defined as, two triangles are congruent if the two angles and the included side of one are respectively equal to the two angles and the included side of the other.
Then,
(i) ∠ATR = ∠PNE
(ii) ∠RAT = ∠EPN
3. You have to show that ΔAMP ≅ ΔAMQ.
In the following proof, supply the missing reasons.
| Steps | Reasons |
| (i) PM = QM | (i) … |
| (ii) ∠PMA = ∠QMA | (ii) … |
| (iii) AM = AM | (iii) … |
| (iv) ΔAMP ≅ ΔAMQ | (iv) … |

Solution:-
| Steps | Reasons |
| (i) PM = QM | (i) From the given figure |
| (ii) ∠PMA = ∠QMA | (ii) From the given figure |
| (iii) AM = AM | (iii) Common side for the both triangles |
| (iv) ΔAMP ≅ ΔAMQ | (iv) By SAS congruence property:- Two triangles are congruent if the two sides and the included angle of one are respectively equal to the two sides and the included angle of the other. |
4. In ΔABC, ∠A = 30o, ∠B = 40o and ∠C = 110o
In ΔPQR, ∠P = 30o, ∠Q = 40o and ∠R = 110o
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified? Why or Why not?
Solution:-
No, because the two triangles with equal corresponding angles need not be congruent. In such a correspondence, one of them can be enlarged copy of the other.
5. In the figure, the two triangles are congruent. The corresponding parts are marked. We can write ΔRAT ≅ ?

Solution:-
From the given figure,
We may observe that,
∠TRA = ∠OWN
∠TAR = ∠NOW
∠ATR = ∠ONW
Hence, ΔRAT ≅ ΔWON
6. Complete the congruence statement:

ΔBCA ≅ ΔQRS ≅
Solution:-
First consider the ΔBCA and ΔBTA
From the figure, it is given that,
BT = BC
Then,
BA is common side for the ΔBCA and ΔBTA
Hence, ΔBCA ≅ ΔBTA
Similarly,
Consider the ΔQRS and ΔTPQ
From the figure, it is given that
PT = QR
TQ = QS
PQ = RS
Hence, ΔQRS ≅ ΔTPQ
7. In a squared sheet, draw two triangles of equal areas such that
(i) The triangles are congruent.
(ii) The triangles are not congruent.
What can you say about their perimeters?
Solution:-
(ii)

In the above figure, ΔABC and ΔDEF have equal areas.
And also, ΔABC ≅ ΔDEF
So, we can say that perimeters of ΔABC and ΔDEF are equal.
(ii)

In the above figure, ΔLMN and ΔOPQ
ΔLMN is not congruent to ΔOPQ
So, we can also say that their perimeters are not same.
8. Draw a rough sketch of two triangles such that they have five pairs of congruent parts but still the triangles are not congruent.
Solution:-
Let us draw triangles LMN and FGH.

In the above figure, all angles of two triangles are equal. But, out of three sides only two sides are equal.
Hence, ΔLMN is not congruent to ΔFGH.
9. If ΔABC and ΔPQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?

Solution:-
By observing the given figure, we can say that
∠ABC = ∠PQR
∠BCA = ∠PRQ
The other additional pair of corresponding part is BC = QR
∴ ΔABC ≅ ΔPQR
10. Explain, why ΔABC ≅ ΔFED

Solution:-
From the figure, it is given that,
∠ABC = ∠DEF = 90o
∠BAC = ∠DFE
BC = DE
By ASA congruence property, two triangles are congruent if the two angles and the included side of one are respectively equal to the two angles and the included side of the other.
ΔABC ≅ ΔFED
Frequently Asked Questions on NCERT Solutions for Class 7 Maths Chapter 7
Is NCERT Solutions for Class 7 Maths Chapter 7 important from exam point of view?
Yes, all the chapters of NCERT Solutions for Class 7 Maths Chapter 7 are important from an exam perspective. As this chapter explains congruence of triangles which is important for board exams as well as for higher studies. So studying these concepts makes learning easier for students. Most of the questions in exams come from this chapter.
Give me a short summary on NCERT Solutions for Class 7 Maths Chapter 7?
NCERT Solutions for Class 7 Maths Chapter 7 has 2 exercises. The chapter deals with different topics related to the probability that includes:
1. Congruence of Plane Figures
2.Congruence Among Line Segments.
3. Congruence of Angles
4. Congruence of Triangles
5. Criteria For Congruence of Triangles
6. Congruence Among Right-Angled Triangles.
What are the key benefits of learning NCERT Solutions for Class 7 Maths Chapter 7?
The answers of NCERT Solutions for Class 7 Maths Chapter 7 have come in handy. This makes it easy to clear all the doubts related to congruence of triangles. Easily solve all the questions easily which have been given for assignments by the Class 7 students.