NCERT Solutions For Class 6 Maths Chapter 5 : Understanding Elementary Shapes
NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes are available here so that students can learn better and more effectively. These materials in PDF format can be downloaded by the students to practise offline. BYJU’S offers online learning materials such as notes, question papers, exemplar problems, etc. for almost all the classes which students can use as worksheets to prepare well for exams. NCERT Solutions for Class 6 Chapter 5 Understanding Elementary Shapes are provided here to support the students in their exam preparation. Practising these solved problems of NCERT Class 6 Chapter 5 will help the students in understanding the techniques to solve the different types of questions.Chapter 5 Understanding ElementaryExercise 5.1
NCERT Solutions for Class 6 Chapter 5: Understanding Elementary Shapes Download PDF





























All the learning materials available in BYJU’S are designed by our subject experts with respect to CBSE syllabus. The NCERT Solutions for class 6 Maths contain solved questions which have been described in the best possible methods. Students can use these methods to solve problems in textbooks, sample papers and previous year question papers.
NCERT Solutions Class 6 Maths Chapter 5 – Understanding Elementary Shapes
Access NCERT Solutions for Class 6 Chapter 5: Understanding Elementary Shapes
Exercise 5.1 page no: 88
1. What is the disadvantage in comparing line segments by mere observation?
Solutions:
By mere observation we can’t compare the line segments with slight difference in their length. We can’t say which line segment is of greater length. Hence, the chances of errors due to improper viewing are more.
2. Why is it better to use a divider than a ruler, while measuring the length of a line segment?
Solutions:
While using a ruler, chances of error occur due to thickness of the ruler and angular viewing. Hence, using divider accurate measurement is possible.
3. Draw any line segment, say . Take any point C lying in between A and B. Measure the lengths of AB, BC and AC. Is AB = AC + CB?
Solutions:
Since given that point C lie in between A and B. Hence, all points are lying on same line segment![]() . Therefore for every situation in which point C is lying in between A and B we may say that
. Therefore for every situation in which point C is lying in between A and B we may say that
AB = AC + CB
For example:
AB is a line segment of length 7 cm and C is a point between A and B such that AC = 3 cm and CB = 4 cm.
Hence, AC + CB = 7 cm
Since, AB = 7 cm
∴ AB = AC + CB is verified.
4. If A, B, C are three points on a line such that AB = 5 cm, BC = 3 cm and AC = 8 cm, which one of them lies between the other two?
Solutions:
Given AB = 5 cm
BC = 3 cm
AC = 8 cm
Now, it is clear that AC = AB + BC
Hence, point B lies between A and C.
5. Verify, whether D is the mid point of .

Solutions:
Since, it is clear from the figure that AD = DG = 3 units. Hence, D is the midpoint of
6. If B is the mid point of and C is the mid point of , where A, B, C, D lie on a straight line, say why AB = CD?
Solutions:

Given
B is the midpoint of AC. Hence, AB = BC (1)
C is the midpoint of BD. Hence, BC = CD (2)
From (1) and (2)
AB = CD is verified
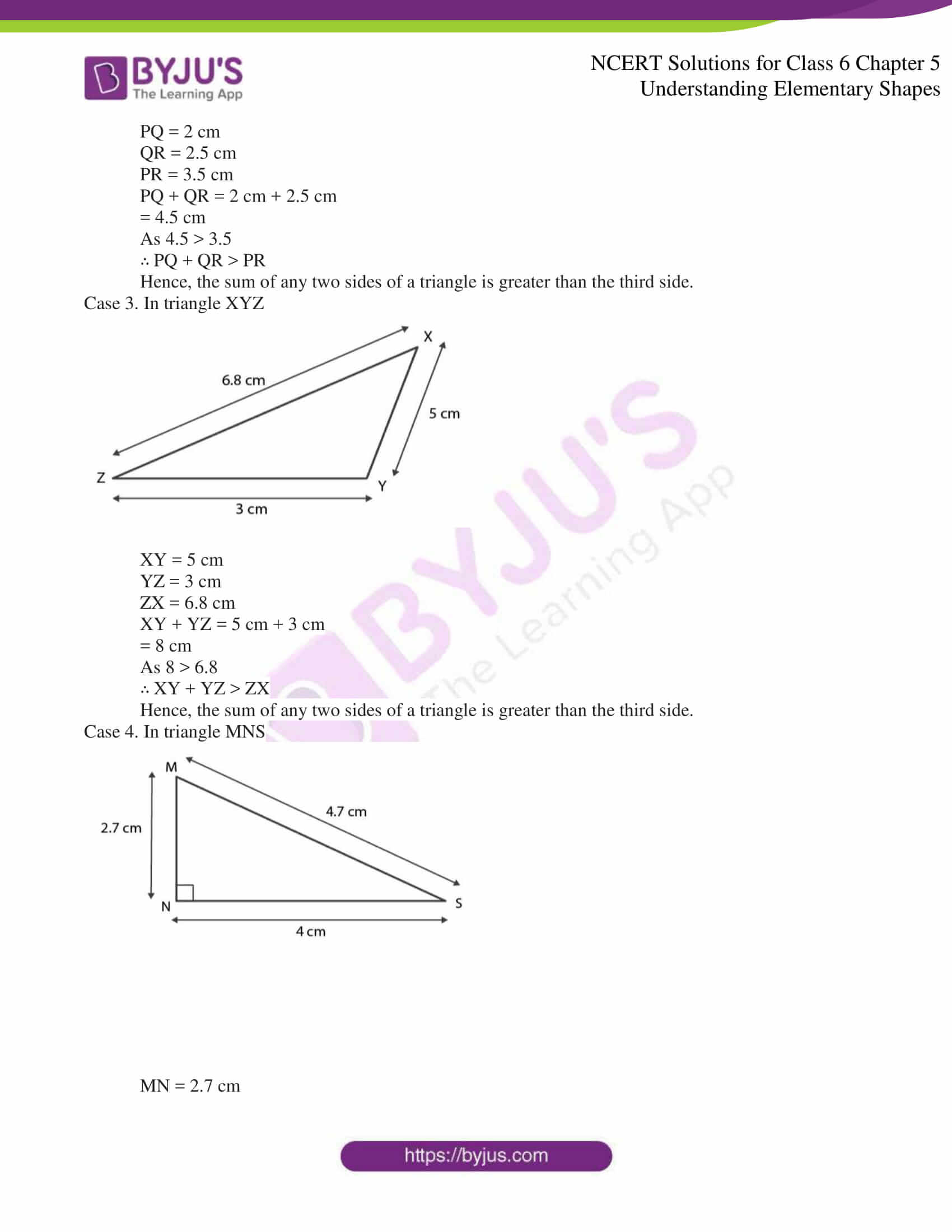
7. Draw five triangles and measure their sides. Check in each case, if the sum of the lengths of any two sides is always less than the third side.
Solutions:
Case 1. In triangle ABC

AB= 2.5 cm
BC = 4.8 cm and
AC = 5.2 cm
AB + BC = 2.5 cm + 4.8 cm
= 7.3 cm
As 7.3 > 5.2
∴ AB + BC > AC
Hence, the sum of any two sides of a triangle is greater than the third side.
Case 2. In triangle PQR

PQ = 2 cm
QR = 2.5 cm
PR = 3.5 cm
PQ + QR = 2 cm + 2.5 cm
= 4.5 cm
As 4.5 > 3.5
∴ PQ + QR > PR
Hence, the sum of any two sides of a triangle is greater than the third side.
Case 3. In triangle XYZ

XY = 5 cm
YZ = 3 cm
ZX = 6.8 cm
XY + YZ = 5 cm + 3 cm
= 8 cm
As 8 > 6.8
∴ XY + YZ > ZX
Hence, the sum of any two sides of a triangle is greater than the third side.
Case 4. In triangle MNS

MN = 2.7 cm
NS = 4 cm
MS = 4.7 cm
MN + NS = 2.7 cm + 4 cm
6.7 cm
As 6.7 > 4.7
∴ MN + NS > MS
Hence, the sum of any two sides of a triangle is greater than the third side.
Case 5. In triangle KLM

KL = 3.5 cm
LM = 3.5 cm
KM = 3.5 cm
KL + LM = 3.5 cm + 3.5 cm
= 7 cm
As 7 cm > 3.5 cm
∴ KL + LM > KM
Hence, the sum of any two sides of a triangle is greater than the third side.
Therefore we conclude that the sum of any two sides of a triangle is always greater than the third side.
Exercise 5.2 page no: 91
1. What fraction of a clockwise revolution does the hour hand of a clock turn through, when it goes from
(a) 3 to 9
(b) 4 to 7
(c) 7 to 10
(d) 12 to 9
(e) 1 to 10
(f) 6 to 3
Solutions:
We know that in one complete clockwise revolution, hour hand will rotate by 3600
(a) When hour hand goes from 3 to 9 clockwise, it will rotate by 2 right angles or 1800
∴ Fraction = 1800 / 3600
= 1 / 2

(b) When hour hand goes from 4 to 7 clockwise, it will rotate by 1 right angle or 900
∴ Fraction = 900 / 3600
= 1 / 4

(c) When hour hand goes from 7 to 10 clockwise, it will rotate by 1 right angle or 900
∴ Fraction = 900 / 3600
= 1 / 4

(d) When hour hand goes from 12 to 9 clockwise, it will rotate by 3 right angles or 2700
∴ Fraction = 2700 / 3600
= 3 / 4

(e) When hour hand of a clock goes from 1 to 10 clockwise, it will rotate by 3 right angles or 2700
∴ Fraction = 2700 / 3600
= 3 / 4

(f) When hour hand goes from 6 to 3 clockwise, it will rotate by 3 right angles or 2700
∴ Fraction = 2700 / 3600
= 3 / 4

2. Where will the hand of a clock stop if it
(a) starts at 12 and makes 1 / 2 of a revolution, clockwise?
(b) starts at 2 and makes 1 / 2 of a revolution, clockwise?
(c) starts at 5 and makes 1 / 4 of a revolution, clockwise?
(d) starts at 5 and makes 3 / 4 of a revolution, clockwise?
Solutions:
We know that one complete clockwise revolution, hour hand will rotate by 3600
(a) When hour hand of a clock starts at 12 and makes 1 / 2 revolution clockwise, it will rotate by 1800.
Hence, the hour hand of a clock will stop at 6.

(b) When hour hand of a clock starts at 2 and makes 1 / 2 revolution clockwise, it will rotate by 1800
Hence, the hour hand of a clock will stop at 8.

(c) When hour hand of a clock starts at 5 and makes 1 / 4 revolution clockwise, it will rotate by 900
Hence, hour hand of a clock will stop at 8.

(d) When hour hand of a clock starts at 5 and makes 3 / 4 revolution clockwise, it will rotate by 2700
Hence, hour hand of a clock will stop at 2

3. Which direction will you face if you start facing
(a) east and make 1 / 2 of a revolution clockwise?
(b) east and make 1 ½ of a revolution clockwise?
(c) west and make 3 / 4 of a revolution anti – clockwise?
(d) south and make one full revolution?
(should we specify clockwise or anti – clockwise for this last question? Why not?)
Solutions:
Revolving one complete round in clockwise or in anti – clockwise direction we will revolve by 3600 and two adjacent directions are at 900 or 1 / 4 of a complete revolution away from each other.
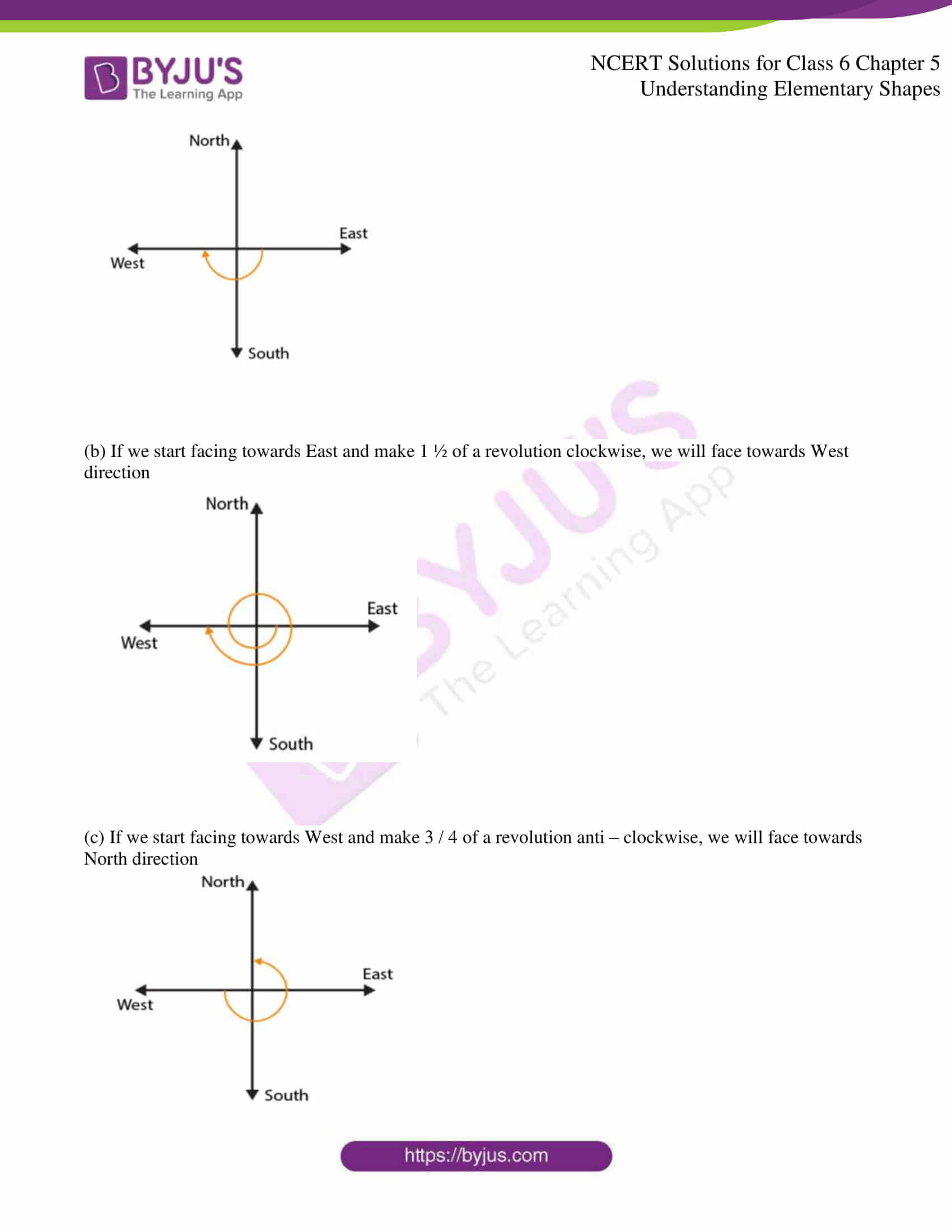
(a) If we start facing towards East and make 1 / 2 of a revolution clockwise, we will face towards West direction.

(b) If we start facing towards East and make 1 ½ of a revolution clockwise, we will face towards West direction

(c) If we start facing towards West and make 3 / 4 of a revolution anti – clockwise, we will face towards North direction

(d) If we start facing South and make one full revolution, again we will face the South direction.

In case of revolving 1 complete revolution, either clockwise or anti-clockwise we will be back at the original position.
4. What part of a revolution have you turned through if you stand facing
(a) east and turn clockwise to face north?
(b) south and turn clockwise to face east
(c) west and turn clockwise to face east?
Solutions:
By revolving one complete revolution either in clockwise or in anti-clockwise direction, we will revolve by 3600 and two adjacent directions are at 900 or 1 / 4 of a complete revolution away from each other
(a) If we start facing towards East and turn clockwise to face North, we have to make 3 / 4 of a revolution

(b) If we start facing towards South and turn clockwise to face East, we have to make 3 / 4 of a revolution

(c) If we start facing towards West and turn clockwise to face East, we have to make 1 / 2 of a revolution

5. Find the number of right angles turned through by the hour hand of a clock when it goes from
(a) 3 to 6
(b) 2 to 8
(c) 5 to 11
(d) 10 to 1
(e) 12 to 9
(f) 12 to 6
Solutions:
The hour hand of a clock revolves by 3600 or it covers 4 right angles in one complete revolution
(a) If hour hand of a clock goes from 3 to 6, it revolves by 900 or 1 right angle

(b) If hour hand of a clock goes from 2 to 8, it revolves by 1800 or 2 right angles

(c) If hour hand of a clock goes from 5 to 11, it revolves by 1800 or 2 right angles

(d) If hour hand of a clock goes from 10 to 1, it revolves by 900 or 1 right angle

(e) If hour hand of a clock goes from 12 to 9, it revolves by 2700 or 3 right angles

(f) If hour hand of a clock goes from 12 to 6, it revolves by 1800 or 2 right angles

6. How many right angles do you make if you start facing
(a) south and turn clockwise to west?
(b) north and turn anti – clockwise to east?
(c) west and turn to west?
(d) south and turn to north?
Solutions:
By revolving one complete round in either clockwise or anti-clockwise direction, we will revolve by 3600 and two adjacent directions are at 900 away from each other.
(a) If we start facing towards South and turn clockwise to West, we have to make one right angle

(b) If we start facing towards North and turn anti-clockwise to East, we have to make 3 right angles

(c) If we start facing towards West and turn to West, we have to make one complete round or 4 right angles

(d) If we start facing towards South and turn to North, we have to make 2 right angles

7. Where will the hour hand of a clock stop if it starts
(a) from 6 and turns through 1 right angle?
(b) from 8 and turns through 2 right angles?
(c) from 10 and turns through 3 right angles?
(d) from 7 and turns through 2 straight angles?
Solutions:
We know that in 1 complete revolution in either clockwise or anticlockwise direction, hour hand of a clock will rotate by 3600 or 4 right angles
(a) If hour hand of a clock starts from 6 and turns through 1 right angle, it will stop at 9

(b) If hour hand of a clock starts from 8 and turns through 2 right angles, it will stop at 2

(c) If hour hand of a clock starts from 10 and turns through 3 right angles, it will stop at 7

(d) If hour hand of a clock starts from 7 and turns through 2 straight angles, it will stop at 7

Exercise 5.3 page NO: 94
1. Match the following:
(i) Straight angle (a) Less than one-fourth of a revolution
(ii) Right angle (b) More than half a revolution
(iii) Acute angle (c) Half of a revolution
(iv) Obtuse angle (d) One-fourth of a revolution
(v) Reflex angle (e) Between 1 / 4 and 1 / 2 of a revolution
(f) One complete revolution
Solutions:
(i) Straight angle = 1800 or half of a revolution
Hence, (c) is correct answer
(ii) Right angle = 900 or one-fourth of a revolution
Hence, (d) is correct answer
(iii) Acute angle = less than 900 or less than one-fourth of a revolution
Hence, (a) is correct answer
(iv) Obtuse angle = more than 900 but less than 1800 or between 1 / 4 and 1 / 2 of a revolution
Hence, (e) is correct answer
(v) Reflex angle = more than 1800 but less than 3600 or more than half a revolution
Hence, (b) is correct answer
2. Classify each one of the following angles as right, straight, acute, obtuse or reflex:

Solutions:
(i) The given angle is acute angle it measures less than 900
(ii) The given angle is obtuse angle as it measures more than 900 but less than 1800
(iii) The given angle is right angle as it measures 900
(iv) The given angle is reflex angle as it measures more than 1800 but less than 3600
(v) The given angle is straight angle as it measures 1800
(vi) The given angle is acute angle as it measures less than 900
Exercise 5.4 page no: 97
1. What is the measure of
(i) a right angle?
(ii) a straight angle
Solutions:
(i) The measure of a right angle is 900
(ii) The measure of a straight angle is 1800
2. Say True or False:
(a) The measure of an acute angle < 900
(b) The measure of an obtuse angle < 900
(c) The measure of a reflex angle > 1800
(d) The measure of one complete revolution = 3600
(e) If m ∠A = 530 and m ∠B = 350, then m ∠A > m ∠B.
Solutions:
(a) True, the measure of an acute angle is less than 900
(b) False, the measure of an obtuse angle is more than 900 but less than 1800
(c) True, the measure of a reflex angle is more than 1800
(d) True, the measure of one complete revolution is 3600
(e) True, ∠A is greater than ∠B
3. Write down the measures of
(a) some acute angles
(b) some obtuse angles
(give at least two examples of each)
Solutions:
(a) The measures of an acute angle are 500, 650
(b) The measures of obtuse angle are 1100, 1750
4. Measures the angles given below using the protractor and write down the measure.

Solutions:
(a) The measure of an angle is 450
(b) The measure of an angle is 1200
(c) The measure of an angle is 900
(d) The measures of an angles are 600, 900 and 1300
5. Which angle has a large measure? First estimate and then measure.
Measure of Angle A =
Measure of Angle B =

Solutions:
The measure of angle A is 400
The measure of angle B is 680
∠B has a large measure than ∠A
6. From these two angles which has larger measure? Estimate and then confirm by measuring them.

Solutions:
The measures of these angles are 450 and 550. Hence, angle shown in second figure is greater.
7. Fill in the blanks with acute, obtuse, right or straight:
(a) An angle whose measure is less than that of a right angle is _____
(b) An angle whose measure is greater than that of a right angle is ____
(c) An angle whose measure is the sum of the measures of two right angles is _______
(d) When the sum of the measures of two angles is that of a right angle, then each one of them is _____
(e) When the sum of the measures of two angles is that of a straight angle and if one of them is acute then the other should be ______
Solutions:
(a) An angle whose measure is less than that of a right angle is acute angle
(b) An angle whose measure is greater than that of a right angle is obtuse angle (but less than 1800)
(c) An angle whose measure is the sum of the measures of two right angles is straight angle
(d) When the sum of the measures of two angles is that of a right angle, then each one of them is acute angle
(e) When the sum of the measures of two angles is that of a straight angle and if one of them is acute then the other should be obtuse angle.
8. Find the measure of the angle shown in each figure. (First estimate with your eyes and then find the actual measure with a protractor).

Solutions:
The measures of the angles shown in above figure are 400, 1300, 650 and 1350
9. Find the angle measure between the hands of the clock in each figure:

Solutions:
The angle measure between the hands of the clock are 900, 300 and 1800
10. Investigate
In the given figure, the angle measure 300. Look at the same figure through a magnifying glass. Does the angle becomes larger? Does the size of the angle change?

Solutions:
The measure of an angle will not change by viewing through a magnifying glass
11. Measure and classify each angle:

| Angle | Measure | Type |
| ∠AOB | ||
| ∠AOC | ||
| ∠BOC | ||
| ∠DOC | ||
| ∠DOA | ||
| ∠DOB |
Solutions:
| Angle | Measure | Type |
| ∠AOB | 400 | Acute |
| ∠AOC | 1250 | Obtuse |
| ∠BOC | 850 | Acute |
| ∠DOC | 950 | Obtuse |
| ∠DOA | 1400 | Obtuse |
| ∠DOB | 1800 | Straight |
Exercise 5.5 page no: 100
1. Which of the following are models for perpendicular lines:
(a) The adjacent edges of a table top.
(b) The lines of a railway track.
(c) The line segments forming the letter ‘L’.
(d) The letter V.
Solutions:
(a) The adjacent edges of a table top are perpendicular to each other.
(b) The lines of a railway track are parallel to each other.
(c) The line segments forming the letter ‘L’ are perpendicular to each other
(d) The sides of letter V are inclined forming an acute angle.
Therefore (a) and (c) are models for perpendicular lines.
2. Let be the perpendicular to the line segment . Let and intersect in the point A. What is the measure of ∠PAY?
Solutions:

From the figure it is clear that the measure of ∠PAY is 900
3. There are two set squares in your box. What are the measures of the angles that are formed at their corners? Do they have any angle measure that is common?
Solutions:
The measure of angles in one set square are 300, 600 and 900
The other set square has a measure of angles 450, 450 and 900
Yes, the angle of measure 900 is common in between them
4. Study the diagram. The line l is perpendicular to line m
(a) Is CE = EG?

(b) Does PE bisect CG?
(c) Identify any two line segments for which PE is the perpendicular bisector.
(d) Are these true?
(i) AC > FG
(ii) CD = GH
(iii) BC < EH.
Solutions:
(a) Yes, since, CE = 2 units and EG = 2 units respectively
(b) Yes. Since, CE = EG as both are of 2 units. Hence PE bisect CG
(c) ![]() and
and ![]() are the line segments for which PE is the perpendicular bisector
are the line segments for which PE is the perpendicular bisector
(d) (i) True. Since AC = 2 units and FG = 1 unit
∴ AC > FG
(ii) True because both are of 1 unit
(iii) True. Since, BC = 1 unit and EH = 3 units
∴ BC < EH
Exercise 5.6 page no: 103
1. Name the types of following triangles:
(a) Triangle with lengths of sides 7 cm, 8 cm and 9 cm.
(b) ∆ABC with AB = 8.7 cm, AC = 7 cm and BC = 6 cm.
(c) ∆PQR such that PQ = QR = PR = 5 cm.
(d) ∆DEF with ∠D = 90°
(e) ∆XYZ with ∠Y = 90° and XY = YZ.
(f) ∆LMN with ∠L = 30°, ∠M = 70° and ∠N = 80°.
Solutions:
(a) Scalene triangle
(b) Scalene triangle
(c) Equilateral triangle
(d) Right angled triangle
(e) Right angled isosceles triangle
(f) Acute angled triangle
2. Match the following:
Measures of Triangle Type of Triangle
(i) 3 sides of equal length (a) Scalene
(ii) 2 sides of equal length (b) Isosceles right angled
(iii) All sides are of different length (c) Obtuse angled
(iv) 3 acute angles (d) Right angled
(v) 1 right angle (e) Equilateral
(vi) 1 obtuse angle (f) Acute angled
(vii) 1 right angle with two sides of equal length (g) Isosceles
Solutions:
(i) Equilateral triangle
(ii) Isosceles triangle
(iii) Scalene triangle
(iv) Acute angled triangle
(v) Right angled triangle
(vi) Obtuse angled triangle
(vii) Isosceles right angled triangle
3. Name each of the following triangles in two different ways: (you may judge the nature of the angle by observation)

Solutions:
(i) Acute angled and isosceles triangle
(ii) Right angled and scalene triangle
(iii) Obtuse angled and isosceles triangle
(iv) Right angled and isosceles triangle
(v) Equilateral and acute angled triangle
(vi) Obtuse angled and scalene triangle
4. Try to construct triangles using match sticks. Some are shown here. Can you make a triangle with
(a) 3 matchsticks?
(b) 4 matchsticks?
(c) 5 matchsticks?
(d) 6 matchsticks?
(Remember you have to use all the available matchsticks in each case)
Name the type of triangle in each case. If you cannot make a triangle, think of reasons for it

Solutions:
(a) By using three match sticks we may make a triangle as shown below
The above triangle is an equilateral triangle
(b) By using 4 match sticks we cannot make a triangle, since we know that sum of the lengths of any two sides of a triangle is always greater than the third side.
(c) By using 5 match sticks we may make a triangle as shown below

The above triangle is an isosceles triangle
(d) By using 6 match sticks we may make a triangle as shown below

The above triangle is an equilateral triangle
Exercise 5.7 page no: 106
1. Say True or False:
(a) Each angle of a rectangle is a right angle.
(b) The opposite sides of a rectangle are equal in length.
(c) The diagonals of a square are perpendicular to one another.
(d) All the sides of a rhombus are of equal length.
(e) All the sides of a parallelogram are of equal length.
(f) The opposite sides of a trapezium are parallel.
Solutions:
(a) True, each angle of a rectangle is a right angle
(b) True, the opposite sides of a rectangle are equal in length.
(c) True, the diagonals of a square are perpendicular to one another
(d) True, all the sides of a rhombus are of equal length
(e) False, all the sides of a parallelogram are not equal
(f) False, the opposite sides of a trapezium are not parallel
2. Give reasons for the following:
(a) A square can be thought of as a special rectangle.
(b) A rectangle can be thought of as a special parallelogram.
(c) A square can be thought of as a special rhombus.
(d) Squares, rectangles, parallelograms are all quadrilaterals.
(e) Square is also a parallelogram.
Solutions:
(a) A rectangle in which all the interior angles are of same measure i.e 900 and only opposite sides of the rectangle are of same length whereas in square all the interior angles are of 900 and all the sides of the square are of same length. Hence, a rectangle with all sides equal becomes a square. Therefore square is a special rectangle.
(b) In a parallelogram opposite sides are parallel and equal. In a rectangle opposite sides are parallel and equal. The interior angles of the rectangle are of same measure i.e 900. Hence, a parallelogram with each angle as right angle becomes a square. Therefore a rectangle is a special parallelogram
(c) All sides of a rhombus and square are equal but in case of square all interior angles are of 900. A rhombus with each angle as right angle becomes a square. Therefore a square is a special rhombus
(d) Since, all are closed figures with 4 line segments. Hence all are quadrilaterals
(e) Opposite sides of a parallelogram are equal and parallel whereas in a square opposite sides are parallel and all 4 sides are of same length. Therefore a square is a special parallelogram.
3. A figure is said to be regular if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?
Solutions:
Square is a regular quadrilateral because all the interior angles are of 900 and all sides are of same length.
Exercise 5.8 page no: 108
1. Examine whether the following are polygons. If any one among them is not, say why?

Solutions:
(i) It is not a closed figure. Hence, it is not a polygon.
(ii) It is a polygon made of six sides
(iii) No it is not a polygon because it is not made of line segments.
(iv) It is not a polygon as it is not made of line segments.
2. Name each polygon.

Make two more examples of each of these.
(a) It is a closed figure and is made of four line segments. Hence, the given figure is a quadrilateral. Two more examples are

(b) The given figure is a triangle as it is a closed figure with 3 line segments. Two more examples are

(c) The given figure is a pentagon as this closed figure made of 5 line segments. Two more examples are

(d) The given figure is an octagon as it is a closed figure made of 8 line segments. Two more examples are

3. Draw a rough sketch of a regular hexagon. Connecting any three of its vertices, draw a triangle. Identify the type of the triangle you have drawn.
Solutions:
We can draw an isosceles triangle by joining three of vertices of a hexagon as shown in below figure

4. Draw a rough sketch of a regular octagon. (Use squared paper if you wish). Draw a rectangle by joining exactly four of the vertices of the octagon.
Solution:
The below figure is a regular octagon in which a rectangle is drawn by joining four of the vertices of the octagon.

5. A diagonal is a line segment that joins any two vertices of the polygon and is not a side of the polygon. Draw a rough sketch of a pentagon and draw its diagonals.
Solutions:
From the figure we may find AC, AD, BD, BE and CE are the diagonals

Exercise 5.9 page no: 111
1. Match the following:
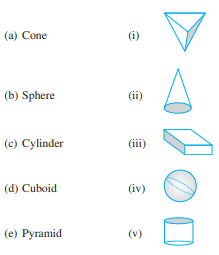
Give two new examples of each shape.
Solutions:
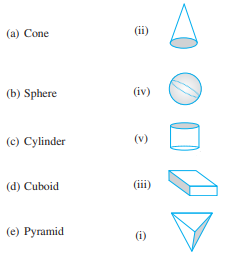
(a) An ice cream cone and birthday cap are examples of cone
(b) Cricket ball and tennis ball are examples of sphere
(c) A road roller and lawn roller are examples of cylinder
(d) A book and a brick are examples of cuboid
(e) A diamond and Egypt pyramids are examples of pyramid
2. What shape is
(a) Your instrument box?
(b) A brick?
(c) A match box?
(d) A road-roller?
(e) A sweet laddu?
Solutions:
(a) The shape of an instrument box is cuboid
(b) The shape of a brick is cuboid
(c) The shape of a match box is cuboid
(d) The shape of a road roller is cylinder
(e) The shape of a sweet laddu is sphere
Frequently Asked Questions on NCERT Solutions for Class 6 Maths Chapter 5
Define angles and its types covered under NCERT Solutions for Class 6 Maths Chapter 5?
An angle is made up of any two rays which have the same endpoint or starting point. It can be better understood by the movement of clock-hands. When a clock hand moves, it forms an angle. To measure the angle, a protractor is used. It should be noted that a straight angle is 180 degrees while a right angle is 90 degrees.
Based on the degree, an angle can be classified into 3 main types:
1. Acute angle: When an angle measure is less than a right angle, it is called an acute angle.
2. Obtuse angle: When an angle measures more than a right angle but less than a straight angle, it is called an obtuse angle.
3. Reflex angle: When an angle measures more than a straight angle, it is called a reflex angle.
Explain solid shapes covered under NCERT Solutions for Class 6 Maths.
A solid shape or three-dimensional shape (3D shape) can be defined as the objects which can be measured in three directions i.e. length, breadth, and height. Examples of 3d shapes are cylinder, cube, cuboid, sphere, etc.
Does BYJU’S give the most reliable answers in Chapter 5 of NCERT Solutions for Class 6 Maths?
The most accurate and reliable NCERT Solutions for Class 6 Maths Chapter 5 are available on BYJU’S. Students can easily download the solutions which are present in PDF format and access to them during their exam preparation. The solutions are framed and compiled by a set of expert faculty who possess numerous years of experience in the respective subjects. The most detailed solutions of the exercise wise problems are curated with the aim of helping students to ace the exam without fear.