NCERT Solutions for Class 9 Maths Chapter 2 Polynomials

NCERT Solutions Class 9 Maths Chapter 2 – Free PDF Download

NCERT Solutions Class 9 Maths Chapter 2 Polynomials are provided here. These NCERT Solutions are created by BYJU’S expert faculties to help students in the preparation of their board exams. These expert faculties solve and provide the NCERT Solutions for Class 9 so that it would help students to solve the problems comfortably. They give a detailed and stepwise explanation of each answer to the problems given in the exercises in the NCERT textbook for Class 9.

In NCERT Solutions for Class 9, students are introduced to a lot of important topics which will be helpful for those who wish to pursue Mathematics as a subject in further classes. Based on these NCERT Solutions. These solutions help students to prepare for their upcoming Board Exams by covering the whole syllabus which follows NCERT guidelines.Chapter 2- Polynomials

Download PDF of NCERT Solutions for Class 9 Maths Chapter 2- Polynomials

Access Answers of NCERT Class 9 Maths Chapter 2 – Polynomials

Exercise 2.1 Page: 32

1. Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer.

(i) 4x²–3x+7

Solution:

The equation 4x²–3x+7 can be written as 4x²–3x¹+7x⁰

Since x is the only variable in the given equation and the powers of x (i.e., 2, 1 and 0) are whole numbers, we can say that the expression 4x²–3x+7 is a polynomial in one variable.

(ii) y²+√2

Solution:

The equation y²+√2 can be written as y²+√2y⁰

Since y is the only variable in the given equation and the powers of y (i.e., 2 and 0) are whole numbers, we can say that the expression y²+√2 is a polynomial in one variable.

(iii) 3√t+t√2

Solution:

The equation 3√t+t√2 can be written as 3t^1/2+√2t

Though, t is the only variable in the given equation, the powers of t (i.e.,1/2) is not a whole number. Hence, we can say that the expression 3√t+t√2 is not a polynomial in one variable.

(iv) y+2/y

Solution:

The equation y+2/y an be written as y+2y^-1

Though, y is the only variable in the given equation, the powers of y (i.e.,-1) is not a whole number. Hence, we can say that the expression y+2/y is not a polynomial in one variable.

(v) x¹⁰+y³+t⁵⁰

Solution:

Here, in the equation x¹⁰+y³+t⁵⁰

Though, the powers, 10, 3, 50, are whole numbers, there are 3 variables used in the expression

x¹⁰+y³+t⁵⁰. Hence, it is not a polynomial in one variable.

2. Write the coefficients of x² in each of the following:

(i) 2+x²+x

Solution:

The equation 2+x²+x can be written as 2+(1)x²+x

We know that, coefficient is the number which multiplies the variable.

Here, the number that multiplies the variable x² is 1

, the coefficients of x² in 2+x²+x is 1.

(ii) 2–x²+x³

Solution:

The equation 2–x²+x³ can be written as 2+(–1)x²+x³

We know that, coefficient is the number (along with its sign, i.e., – or +) which multiplies the variable.

Here, the number that multiplies the variable x² is -1

the coefficients of x² in 2–x²+x³ is -1.

(iii) (/2)x²+x

Solution:

The equation (/2)x² +x can be written as (/2)x² + x

We know that, coefficient is the number (along with its sign, i.e., – or +) which multiplies the variable.

Here, the number that multiplies the variable x² is /2.

the coefficients of x² in (/2)x² +x is /2.

(iii)√2x-1

Solution:

The equation √2x-1 can be written as 0x²+√2x-1 [Since 0x² is 0]

We know that, coefficient is the number (along with its sign, i.e., – or +) which multiplies the variable.

Here, the number that multiplies the variable x²is 0

, the coefficients of x² in √2x-1 is 0.

3. Give one example each of a binomial of degree 35, and of a monomial of degree 100.

Solution:

Binomial of degree 35: A polynomial having two terms and the highest degree 35 is called a binomial of degree 35

Eg.,  3x³⁵+5

Monomial of degree 100: A polynomial having one term and the highest degree 100 is called a monomial of degree 100

Eg.,  4x¹⁰⁰

4. Write the degree of each of the following polynomials:

(i) 5x³+4x²+7x

Solution:

The highest power of the variable in a polynomial is the degree of the polynomial.

Here, 5x³+4x²+7x = 5x³+4x²+7x¹

The powers of the variable x are: 3, 2, 1

the degree of 5x³+4x²+7x is 3 as 3 is the highest power of x in the equation.

(ii) 4–y²

Solution:

The highest power of the variable in a polynomial is the degree of the polynomial.

Here, in 4–y²,

The power of the variable y is 2

the degree of 4–y² is 2 as 2 is the highest power of y in the equation.

(iii) 5t–√7

Solution:

The highest power of the variable in a polynomial is the degree of the polynomial.

Here, in 5t–√7 ,

The power of the variable t is: 1

the degree of 5t–√7 is 1 as 1 is the highest power of y in the equation.

(iv) 3

Solution:

The highest power of the variable in a polynomial is the degree of the polynomial.

Here, 3 = 3×1 = 3× x⁰

The power of the variable here is: 0

the degree of 3 is 0.

5. Classify the following as linear, quadratic and cubic polynomials:

Solution:

We know that,

Linear polynomial: A polynomial of degree one is called a linear polynomial.

Quadratic polynomial: A polynomial of degree two is called a quadratic polynomial.

Cubic polynomial: A polynomial of degree three is called a cubic polynomial.

(i) x²+x

Solution:

The highest power of x²+x is 2

the degree is 2

Hence, x²+x is a quadratic polynomial

(ii) x–x³

Solution:

The highest power of x–x³ is 3

the degree is 3

Hence, x–x³ is a cubic polynomial

(iii) y+y²+4

Solution:

The highest power of y+y²+4 is 2

the degree is 2

Hence, y+y²+4is a quadratic polynomial

(iv) 1+x

Solution:

The highest power of 1+x is 1

the degree is 1

Hence, 1+x is a linear polynomial.

(v) 3t

Solution:

The highest power of 3t is 1

the degree is 1

Hence, 3t is a linear polynomial.

(vi) r²

Solution:

The highest power of r² is 2

the degree is 2

Hence, r²is a quadratic polynomial.

(vii) 7x³

Solution:

The highest power of 7x³ is 3

the degree is 3

Hence, 7x³ is a cubic polynomial.

Exercise 2.2 Page: 34

1. Find the value of the polynomial (x)=5x−4x²+3 

(i) x = 0

(ii) x = – 1

(iii) x = 2

Solution:

Let f(x) = 5x−4x²+3

(i) When x = 0

f(0) = 5(0)-4(0)²+3

= 3

(ii) When x = -1

f(x) = 5x−4x²+3

f(−1) = 5(−1)−4(−1)²+3

= −5–4+3

= −6

(iii) When x = 2

f(x) = 5x−4x²+3

f(2) = 5(2)−4(2)²+3

= 10–16+3

= −3

2. Find p(0), p(1) and p(2) for each of the following polynomials:

(i) p(y)=y²−y+1

Solution:

p(y) = y²–y+1

∴p(0) = (0)²−(0)+1=1

p(1) = (1)²–(1)+1=1

p(2) = (2)²–(2)+1=3

(ii) p(t)=2+t+2t²−t³

Solution:

p(t) = 2+t+2t²−t³

∴p(0) = 2+0+2(0)²–(0)³=2

p(1) = 2+1+2(1)²–(1)³=2+1+2–1=4

p(2) = 2+2+2(2)²–(2)³=2+2+8–8=4

(iii) p(x)=x³

Solution:

p(x) = x³

∴p(0) = (0)³ = 0

p(1) = (1)³ = 1

p(2) = (2)³ = 8

(iv) P(x) = (x−1)(x+1)

Solution:

p(x) = (x–1)(x+1)

∴p(0) = (0–1)(0+1) = (−1)(1) = –1

p(1) = (1–1)(1+1) = 0(2) = 0

p(2) = (2–1)(2+1) = 1(3) = 3

3. Verify whether the following are zeroes of the polynomial, indicated against them.

(i) p(x)=3x+1, x=−1/3

Solution:

For, x = -1/3, p(x) = 3x+1

∴p(−1/3) = 3(-1/3)+1 = −1+1 = 0

∴ -1/3 is a zero of p(x).

(ii) p(x)=5x–π, x = 4/5

Solution:

For, x = 4/5, p(x) = 5x–π

∴ p(4/5) = 5(4/5)- = 4-

∴ 4/5 is not a zero of p(x).

(iii) p(x)=x²−1, x=1, −1

Solution:

For, x = 1, −1;

p(x) = x²−1

∴p(1)=1²−1=1−1 = 0

p(−1)=(-1)²−1 = 1−1 = 0

∴1, −1 are zeros of p(x).

(iv) p(x) = (x+1)(x–2), x =−1, 2

Solution:

For, x = −1,2;

p(x) = (x+1)(x–2)

∴p(−1) = (−1+1)(−1–2)

= (0)(−3) = 0

p(2) = (2+1)(2–2) = (3)(0) = 0

∴−1,2 are zeros of p(x).

(v) p(x) = x², x = 0

Solution:

For, x = 0 p(x) = x²

p(0) = 0² = 0

∴ 0 is a zero of p(x).

(vi) p(x) = lx+m, x = −m/l

Solution:

For, x = -m/l ; p(x) = lx+m

∴ p(-m/l)= l(-m/l)+m = −m+m = 0

∴-m/l is a zero of p(x).

(vii) p(x) = 3x²−1, x = -1/√3 , 2/√3

Solution:

For, x = -1/√3 , 2/√3 ; p(x) = 3x²−1

∴p(-1/√3) = 3(-1/√3)²-1 = 3(1/3)-1 = 1-1 = 0

∴p(2/√3 ) = 3(2/√3)²-1 = 3(4/3)-1 = 4−1=3 ≠ 0

∴-1/√3 is a zero of p(x) but 2/√3  is not a zero of p(x).

(viii) p(x) =2x+1, x = 1/2

Solution:

For, x = 1/2 p(x) = 2x+1

∴ p(1/2)=2(1/2)+1 = 1+1 = 2≠0

∴1/2 is not a zero of p(x).

4. Find the zero of the polynomials in each of the following cases:

(i) p(x) = x+5 

Solution:

p(x) = x+5

⇒ x+5 = 0

⇒ x = −5

∴ -5 is a zero polynomial of the polynomial p(x).

(ii) p(x) = x–5

Solution:

p(x) = x−5

⇒ x−5 = 0

⇒ x = 5

∴ 5 is a zero polynomial of the polynomial p(x).

(iii) p(x) = 2x+5

Solution:

p(x) = 2x+5

⇒ 2x+5 = 0

⇒ 2x = −5

⇒ x = -5/2

∴x = -5/2 is a zero polynomial of the polynomial p(x).

(iv) p(x) = 3x–2 

Solution:

p(x) = 3x–2

⇒ 3x−2 = 0

⇒ 3x = 2

⇒x = 2/3

∴x = 2/3  is a zero polynomial of the polynomial p(x).

(v) p(x) = 3x 

Solution:

p(x) = 3x

⇒ 3x = 0

⇒ x = 0

∴0 is a zero polynomial of the polynomial p(x).

(vi) p(x) = ax, a0

Solution:

p(x) = ax

⇒ ax = 0

⇒ x = 0

∴x = 0 is a zero polynomial of the polynomial p(x).

(vii)p(x) = cx+d, c ≠ 0, c, d are real numbers.

Solution:

p(x) = cx + d

⇒ cx+d =0

⇒ x = -d/c

∴ x = -d/c is a zero polynomial of the polynomial p(x).

Exercise 2.3 Page: 40

1. Find the remainder when x³+3x²+3x+1 is divided by

(i) x+1

Solution:

x+1= 0

⇒x = −1

∴Remainder:

p(−1) = (−1)³+3(−1)²+3(−1)+1

= −1+3−3+1

= 0

(ii) x−1/2

Solution:

x-1/2 = 0

⇒ x = 1/2

∴Remainder:

p(1/2) = (1/2)³+3(1/2)²+3(1/2)+1

= (1/8)+(3/4)+(3/2)+1

= 27/8

(iii) x

Solution:

x = 0

∴Remainder:

p(0) = (0)³+3(0)²+3(0)+1

= 1

(iv) x+π

Solution:

x+π = 0

⇒ x = −π

∴Remainder:

p(0) = (−π)³ +3(−π)²+3(−π)+1

= −π³+3π²−3π+1

(v) 5+2x

Solution:

5+2x=0

⇒ 2x = −5

⇒ x = -5/2

∴Remainder:

(-5/2)³+3(-5/2)²+3(-5/2)+1 = (-125/8)+(75/4)-(15/2)+1

= -27/8

2. Find the remainder when x³−ax²+6x−a is divided by x-a.

Solution:

Let p(x) = x³−ax²+6x−a

x−a = 0

∴x = a

Remainder:

p(a) = (a)³−a(a²)+6(a)−a

= a³−a³+6a−a = 5a

3. Check whether 7+3x is a factor of 3x³+7x.

Solution:

7+3x = 0

⇒ 3x = −7

⇒ x = -7/3

∴Remainder:

3(-7/3)³+7(-7/3) = -(343/9)+(-49/3)

= (-343-(49)3)/9

= (-343-147)/9

= -490/9 ≠ 0

∴7+3x is not a factor of 3x³+7x

Exercise 2.4 Page: 43

1. Determine which of the following polynomials has (x + 1) a factor:

(i) x³+x²+x+1

Solution:

Let p(x) = x³+x²+x+1

The zero of x+1 is -1. [x+1 = 0 means x = -1]

p(−1) = (−1)³+(−1)²+(−1)+1

= −1+1−1+1

= 0

∴By factor theorem, x+1 is a factor of x³+x²+x+1

(ii) x⁴+x³+x²+x+1

Solution:

Let p(x)= x⁴+x³+x²+x+1

The zero of x+1 is -1. . [x+1= 0 means x = -1]

p(−1) = (−1)⁴+(−1)³+(−1)²+(−1)+1

= 1−1+1−1+1

= 1 ≠ 0

∴By factor theorem, x+1 is not a factor of x⁴ + x³ + x² + x + 1

(iii) x⁴+3x³+3x²+x+1 

Solution:

Let p(x)= x⁴+3x³+3x²+x+1

The zero of x+1 is -1.

p(−1)=(−1)⁴+3(−1)³+3(−1)²+(−1)+1

=1−3+3−1+1

=1 ≠ 0

∴By factor theorem, x+1 is not a factor of x⁴+3x³+3x²+x+1

(iv) x³ – x²– (2+√2)x +√2

Solution:

Let p(x) = x³–x²–(2+√2)x +√2

The zero of x+1 is -1.

p(−1) = (-1)³–(-1)²–(2+√2)(-1) + √2 = −1−1+2+√2+√2

= 2√2 ≠ 0

∴By factor theorem, x+1 is not a factor of x³–x²–(2+√2)x +√2

2. Use the Factor Theorem to determine whether g(x) is a factor of p(x) in each of the following cases:

(i) p(x) = 2x³+x²–2x–1, g(x) = x+1

Solution:

p(x) = 2x³+x²–2x–1, g(x) = x+1

g(x) = 0

⇒ x+1 = 0

⇒ x = −1

∴Zero of g(x) is -1.

Now,

p(−1) = 2(−1)³+(−1)²–2(−1)–1

= −2+1+2−1

= 0

∴By factor theorem, g(x) is a factor of p(x).

(ii) p(x)=x³+3x²+3x+1, g(x) = x+2

Solution:

p(x) = x³+3x²+3x+1, g(x) = x+2

g(x) = 0

⇒ x+2 = 0

⇒ x = −2

∴ Zero of g(x) is -2.

Now,

p(−2) = (−2)³+3(−2)²+3(−2)+1

= −8+12−6+1

= −1 ≠ 0

∴By factor theorem, g(x) is not a factor of p(x).

(iii) p(x)=x³–4x²+x+6, g(x) = x–3

Solution:

p(x) = x³–4x²+x+6, g(x) = x -3

g(x) = 0

⇒ x−3 = 0

⇒ x = 3

∴ Zero of g(x) is 3.

Now,

p(3) = (3)³−4(3)²+(3)+6

= 27−36+3+6

= 0

∴By factor theorem, g(x) is a factor of p(x).

3. Find the value of k, if x–1 is a factor of p(x) in each of the following cases:

(i) p(x) = x²+x+k

Solution:

If x-1 is a factor of p(x), then p(1) = 0

By Factor Theorem

⇒ (1)²+(1)+k = 0

⇒ 1+1+k = 0

⇒ 2+k = 0

⇒ k = −2

(ii) p(x) = 2x²+kx+√2

Solution:

If x-1 is a factor of p(x), then p(1)=0

⇒ 2(1)²+k(1)+√2 = 0

⇒ 2+k+√2 = 0

⇒ k = −(2+√2)

(iii) p(x) = kx²–√2x+1

Solution:

If x-1 is a factor of p(x), then p(1)=0

By Factor Theorem

⇒ k(1)²-√2(1)+1=0

⇒ k = √2-1

(iv) p(x)=kx²–3x+k

Solution:

If x-1 is a factor of p(x), then p(1) = 0

By Factor Theorem

⇒ k(1)²–3(1)+k = 0

⇒ k−3+k = 0

⇒ 2k−3 = 0

⇒ k= 3/2

4. Factorize:

(i) 12x²–7x+1

Solution:

Using the splitting the middle term method,

We have to find a number whose sum = -7 and product =1×12 = 12

We get -3 and -4 as the numbers [-3+-4=-7 and -3×-4 = 12]

12x²–7x+1= 12x²-4x-3x+1

= 4x(3x-1)-1(3x-1)

= (4x-1)(3x-1)

(ii) 2x²+7x+3

Solution:

Using the splitting the middle term method,

We have to find a number whose sum = 7 and product = 2×3 = 6

We get 6 and 1 as the numbers [6+1 = 7 and 6×1 = 6]

2x²+7x+3 = 2x²+6x+1x+3

= 2x (x+3)+1(x+3)

= (2x+1)(x+3)

(iii) 6x²+5x-6 

Solution:

Using the splitting the middle term method,

We have to find a number whose sum = 5 and product = 6×-6 = -36

We get -4 and 9 as the numbers [-4+9 = 5 and -4×9 = -36]

6x²+5x-6 = 6x²+9x–4x–6

= 3x(2x+3)–2(2x+3)

= (2x+3)(3x–2)

(iv) 3x²–x–4 

Solution:

Using the splitting the middle term method,

We have to find a number whose sum = -1 and product = 3×-4 = -12

We get -4 and 3 as the numbers [-4+3 = -1 and -4×3 = -12]

3x²–x–4 = 3x²–x–4

= 3x²–4x+3x–4

= x(3x–4)+1(3x–4)

= (3x–4)(x+1)

5. Factorize:

(i) x³–2x²–x+2

Solution:

Let p(x) = x³–2x²–x+2

Factors of 2 are ±1 and ± 2

Now,

p(x) = x³–2x²–x+2

p(−1) = (−1)³–2(−1)²–(−1)+2

= −1−2+1+2

= 0

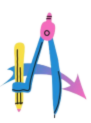
Therefore, (x+1) is the factor of p(x)

Now, Dividend = Divisor × Quotient + Remainder

(x+1)(x²–3x+2) = (x+1)(x²–x–2x+2)

= (x+1)(x(x−1)−2(x−1))

= (x+1)(x−1)(x-2)

(ii) x³–3x²–9x–5

Solution:

Let p(x) = x³–3x²–9x–5

Factors of 5 are ±1 and ±5

By trial method, we find that

p(5) = 0

So, (x-5) is factor of p(x)

Now,

p(x) = x³–3x²–9x–5

p(5) = (5)³–3(5)²–9(5)–5

= 125−75−45−5

= 0

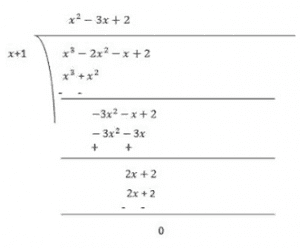
Therefore, (x-5) is the factor of  p(x)

Now, Dividend = Divisor × Quotient + Remainder

(x−5)(x²+2x+1) = (x−5)(x²+x+x+1)

= (x−5)(x(x+1)+1(x+1))

= (x−5)(x+1)(x+1)

(iii) x³+13x²+32x+20

Solution:

Let p(x) = x³+13x²+32x+20

Factors of 20 are ±1, ±2, ±4, ±5, ±10 and ±20

By trial method, we find that

p(-1) = 0

So, (x+1) is factor of p(x)

Now,

p(x)= x³+13x²+32x+20

p(-1) = (−1)³+13(−1)²+32(−1)+20

= −1+13−32+20

= 0

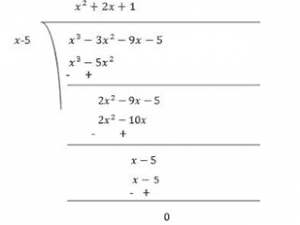
Therefore, (x+1) is the factor of p(x)

Now, Dividend = Divisor × Quotient +Remainder

(x+1)(x²+12x+20) = (x+1)(x²+2x+10x+20)

= (x−5)x(x+2)+10(x+2)

= (x−5)(x+2)(x+10)

(iv) 2y³+y²–2y–1

Solution:

Let p(y) = 2y³+y²–2y–1

Factors = 2×(−1)= -2 are ±1 and ±2

By trial method, we find that

p(1) = 0

So, (y-1) is factor of p(y)

Now,

p(y) = 2y³+y²–2y–1

p(1) = 2(1)³+(1)²–2(1)–1

= 2+1−2

= 0

Therefore, (y-1) is the factor of p(y)

Now, Dividend = Divisor × Quotient + Remainder

(y−1)(2y²+3y+1) = (y−1)(2y²+2y+y+1)

= (y−1)(2y(y+1)+1(y+1))

= (y−1)(2y+1)(y+1)

Exercise 2.5 Page: 48

1. Use suitable identities to find the following products:

(i) (x+4)(x +10) 

Solution:

Using the identity, (x+a)(x+b) = x ²+(a+b)x+ab[Here, a = 4 and b = 10]

We get,

(x+4)(x+10) = x²+(4+10)x+(4×10)

= x²+14x+40

(ii) (x+8)(x –10)     

Solution:

Using the identity, (x+a)(x+b) = x ²+(a+b)x+ab[Here, a = 8 and b = −10]

We get,

(x+8)(x−10) = x²+(8+(−10))x+(8×(−10))

= x²+(8−10)x–80

= x²−2x−80

(iii) (3x+4)(3x–5)

Solution:

Using the identity, (x+a)(x+b) = x ²+(a+b)x+ab[Here, x = 3x, a = 4 and b = −5]

We get,

(3x+4)(3x−5) = (3x)²+[4+(−5)]3x+4×(−5)

= 9x²+3x(4–5)–20

= 9x²–3x–20

(iv) (y²+3/2)(y²-3/2)

Solution:

Using the identity, (x+y)(x–y) = x²–y ²[Here, x = y²and y = 3/2]

We get,

(y²+3/2)(y²–3/2) = (y²)²–(3/2)²

= y⁴–9/4

2. Evaluate the following products without multiplying directly:

(i) 103×107

Solution:

103×107= (100+3)×(100+7)

Using identity, [(x+a)(x+b) = x²+(a+b)x+ab

Here, x = 100

a = 3

b = 7

We get, 103×107 = (100+3)×(100+7)

= (100)²+(3+7)100+(3×7))

= 10000+1000+21

= 11021

(ii) 95×96  

Solution:

95×96 = (100-5)×(100-4)

Using identity, [(x-a)(x-b) = x²-(a+b)x+ab

Here, x = 100

a = -5

b = -4

We get, 95×96 = (100-5)×(100-4)

= (100)²+100(-5+(-4))+(-5×-4)

= 10000-900+20

= 9120

(iii) 104×96

Solution:

104×96 = (100+4)×(100–4)

Using identity, [(a+b)(a-b)= a²-b²]

Here, a = 100

b = 4

We get, 104×96 = (100+4)×(100–4)

= (100)²–(4)²

= 10000–16

= 9984

3. Factorize the following using appropriate identities:

(i) 9x²+6xy+y²

Solution:

9x²+6xy+y² = (3x)²+(2×3x×y)+y²

Using identity, x²+2xy+y² = (x+y)²

Here, x = 3x

y = y

9x²+6xy+y² = (3x)²+(2×3x×y)+y²

= (3x+y)²

= (3x+y)(3x+y)

(ii) 4y²−4y+1

Solution:

4y²−4y+1 = (2y)²–(2×2y×1)+1

Using identity, x² – 2xy + y² = (x – y)²

Here, x = 2y

y = 1

4y²−4y+1 = (2y)²–(2×2y×1)+1²

= (2y–1)²

= (2y–1)(2y–1)

(iii)  x²–y²/100

Solution:

x²–y²/100 = x²–(y/10)²

Using identity, x²-y² = (x-y)(x+y)

Here, x = x

y = y/10

x²–y²/100 = x²–(y/10)²

= (x–y/10)(x+y/10)

4. Expand each of the following, using suitable identities:

(i) (x+2y+4z)²

(ii) (2x−y+z)²

(iii) (−2x+3y+2z)²

(iv) (3a –7b–c)²

(v) (–2x+5y–3z)²

((1/4)a-(1/2)b +1)²

Solution:

(i) (x+2y+4z)²

Using identity, (x+y+z)² = x²+y²+z²+2xy+2yz+2zx

Here, x = x

y = 2y

z = 4z

(x+2y+4z)² = x²+(2y)²+(4z)²+(2×x×2y)+(2×2y×4z)+(2×4z×x)

= x²+4y²+16z²+4xy+16yz+8xz

(ii) (2x−y+z)² 

Using identity, (x+y+z)² = x²+y²+z²+2xy+2yz+2zx

Here, x = 2x

y = −y

z = z

(2x−y+z)² = (2x)²+(−y)²+z²+(2×2x×−y)+(2×−y×z)+(2×z×2x)

= 4x²+y²+z²–4xy–2yz+4xz

(iii) (−2x+3y+2z)²

Solution:

Using identity, (x+y+z)² = x²+y²+z²+2xy+2yz+2zx

Here, x = −2x

y = 3y

z = 2z

(−2x+3y+2z)² = (−2x)²+(3y)²+(2z)²+(2×−2x×3y)+(2×3y×2z)+(2×2z×−2x)

= 4x²+9y²+4z²–12xy+12yz–8xz

(iv) (3a –7b–c)²

Solution:

Using identity (x+y+z)² = x²+y²+z²+2xy+2yz+2zx

Here, x = 3a

y = – 7b

z = – c

(3a –7b– c)² = (3a)²+(– 7b)²+(– c)²+(2×3a ×– 7b)+(2×– 7b ×– c)+(2×– c ×3a)

= 9a² + 49b² + c²– 42ab+14bc–6ca

(v) (–2x+5y–3z)²

Solution:

Using identity, (x+y+z)² = x²+y²+z²+2xy+2yz+2zx

Here, x = –2x

y = 5y

z = – 3z

(–2x+5y–3z)² = (–2x)²+(5y)²+(–3z)²+(2×–2x × 5y)+(2× 5y×– 3z)+(2×–3z ×–2x)

= 4x²+25y² +9z²– 20xy–30yz+12zx

(vi) ((1/4)a-(1/2)b+1)²

Solution:

Using identity, (x+y+z)² = x²+y²+z²+2xy+2yz+2zx

Here, x = (1/4)a

y = (-1/2)b

z = 1

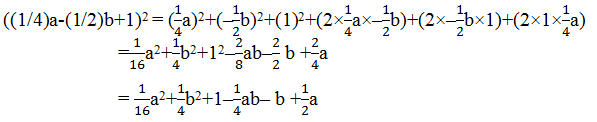
5. Factorize:

(i) 4x²+9y²+16z²+12xy–24yz–16xz

(ii ) 2x²+y²+8z²–2√2xy+4√2yz–8xz

Solution:

(i) 4x²+9y²+16z²+12xy–24yz–16xz

Using identity, (x+y+z)² = x²+y²+z²+2xy+2yz+2zx

We can say that, x²+y²+z²+2xy+2yz+2zx = (x+y+z)²

4x²+9y²+16z²+12xy–24yz–16xz = (2x)²+(3y)²+(−4z)²+(2×2x×3y)+(2×3y×−4z)+(2×−4z×2x)

= (2x+3y–4z)²

= (2x+3y–4z)(2x+3y–4z)

(ii) 2x²+y²+8z²–2√2xy+4√2yz–8xz

Using identity, (x +y+z)² = x²+y²+z²+2xy+2yz+2zx

We can say that, x²+y²+z²+2xy+2yz+2zx = (x+y+z)²

2x²+y²+8z²–2√2xy+4√2yz–8xz

= (-√2x)²+(y)²+(2√2z)²+(2×-√2x×y)+(2×y×2√2z)+(2×2√2×−√2x)

= (−√2x+y+2√2z)²

= (−√2x+y+2√2z)(−√2x+y+2√2z)

6. Write the following cubes in expanded form:

(i) (2x+1)³

(ii) (2a−3b)³

(iii) ((3/2)x+1)³

(iv) (x−(2/3)y)³

Solution:

(i) (2x+1)³

Using identity,(x+y)³ = x³+y³+3xy(x+y)

(2x+1)³= (2x)³+1³+(3×2x×1)(2x+1)

= 8x³+1+6x(2x+1)

= 8x³+12x²+6x+1

(ii) (2a−3b)³

Using identity,(x–y)³ = x³–y³–3xy(x–y)

(2a−3b)³ = (2a)³−(3b)³–(3×2a×3b)(2a–3b)

= 8a³–27b³–18ab(2a–3b)

= 8a³–27b³–36a²b+54ab²

(iii) ((3/2)x+1)³

Using identity,(x+y)³ = x³+y³+3xy(x+y)

((3/2)x+1)³=((3/2)x)³+1³+(3×(3/2)x×1)((3/2)x +1)

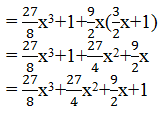
(iv)  (x−(2/3)y)³

Using identity, (x –y)³ = x³–y³–3xy(x–y)

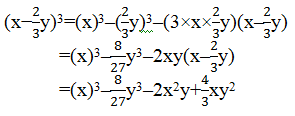
7. Evaluate the following using suitable identities: 

(i) (99)³

(ii) (102)³

(iii) (998)³

Solutions:

(i) (99)³

Solution:

We can write 99 as 100–1

Using identity, (x –y)³ = x³–y³–3xy(x–y)

(99)³ = (100–1)³

= (100)³–1³–(3×100×1)(100–1)

= 1000000 –1–300(100 – 1)

= 1000000–1–30000+300

= 970299

(ii) (102)³

Solution:

We can write 102 as 100+2

Using identity,(x+y)³ = x³+y³+3xy(x+y)

(100+2)³ =(100)³+2³+(3×100×2)(100+2)

= 1000000 + 8 + 600(100 + 2)

= 1000000 + 8 + 60000 + 1200

= 1061208

(iii) (998)³

Solution:

We can write 99 as 1000–2

Using identity,(x–y)³ = x³–y³–3xy(x–y)

(998)³ =(1000–2)³

=(1000)³–2³–(3×1000×2)(1000–2)

= 1000000000–8–6000(1000– 2)

= 1000000000–8- 6000000+12000

= 994011992

8. Factorise each of the following:

(i) 8a³+b³+12a²b+6ab²

(ii) 8a³–b³–12a²b+6ab²

(iii) 27–125a³–135a +225a²   

(iv) 64a³–27b³–144a²b+108ab²

(v) 27p³–(1/216)−(9/2) p²+(1/4)p

Solutions:

(i) 8a³+b³+12a²b+6ab²

Solution:

The expression, 8a³+b³+12a²b+6ab² can be written as (2a)³+b³+3(2a)²b+3(2a)(b)²

8a³+b³+12a²b+6ab² = (2a)³+b³+3(2a)²b+3(2a)(b)²

= (2a+b)³

= (2a+b)(2a+b)(2a+b)

Here, the identity, (x +y)³ = x³+y³+3xy(x+y) is used.

(ii) 8a³–b³–12a²b+6ab²

Solution:

The expression, 8a³–b³−12a²b+6ab² can be written as (2a)³–b³–3(2a)²b+3(2a)(b)²

8a³–b³−12a²b+6ab² = (2a)³–b³–3(2a)²b+3(2a)(b)²

= (2a–b)³

= (2a–b)(2a–b)(2a–b)

Here, the identity,(x–y)³ = x³–y³–3xy(x–y) is used.

(iii) 27–125a³–135a+225a² 

Solution:

The expression, 27–125a³–135a +225a² can be written as 3³–(5a)³–3(3)²(5a)+3(3)(5a)²

27–125a³–135a+225a² =
3³–(5a)³–3(3)²(5a)+3(3)(5a)²

= (3–5a)³

= (3–5a)(3–5a)(3–5a)

Here, the identity, (x–y)³ = x³–y³-3xy(x–y) is used.

(iv) 64a3–27b3–144a²b+108ab²

Solution:

The expression, 64a³–27b³–144a²b+108ab²can be written as (4a)³–(3b)³–3(4a)²(3b)+3(4a)(3b)²

64a³–27b³–144a²b+108ab²=
(4a)³–(3b)³–3(4a)²(3b)+3(4a)(3b)²

=(4a–3b)³

=(4a–3b)(4a–3b)(4a–3b)

Here, the identity, (x – y)³ = x³ – y³ – 3xy(x – y) is used.

(v) 7p³– (1/216)−(9/2) p²+(1/4)p

Solution:

The expression, 27p³–(1/216)−(9/2) p²+(1/4)p

can be written as (3p)³–(1/6)³–3(3p)²(1/6)+3(3p)(1/6)²

27p³–(1/216)−(9/2) p²+(1/4)p =
(3p)³–(1/6)³–3(3p)²(1/6)+3(3p)(1/6)²

= (3p–16)³

= (3p–16)(3p–16)(3p–16)

9. Verify:

(i) x³+y³ = (x+y)(x²–xy+y²)

(ii) x³–y³ = (x–y)(x²+xy+y²)

Solutions:

(i) x³+y³ = (x+y)(x²–xy+y²)

We know that, (x+y)³ = x³+y³+3xy(x+y)

⇒ x³+y³ = (x+y)³–3xy(x+y)

⇒ x³+y³ = (x+y)[(x+y)²–3xy]

Taking (x+y) common ⇒ x³+y³ = (x+y)[(x²+y²+2xy)–3xy]

⇒ x³+y³ = (x+y)(x²+y²–xy)

(ii) x³–y³ = (x–y)(x²+xy+y²) 

We know that,(x–y)³ = x³–y³–3xy(x–y)

⇒ x³−y³ = (x–y)³+3xy(x–y)

⇒ x³−y³ = (x–y)[(x–y)²+3xy]

Taking (x+y) common ⇒ x³−y³ = (x–y)[(x²+y²–2xy)+3xy]

⇒ x³+y³ = (x–y)(x²+y²+xy)

10. Factorize each of the following:

(i) 27y³+125z³

(ii) 64m³–343n³

Solutions:

(i) 27y³+125z³

The expression, 27y³+125z³ can be written as (3y)³+(5z)³

27y³+125z³ = (3y)³+(5z)³

We know that, x³+y³ = (x+y)(x²–xy+y²)

27y³+125z³ = (3y)³+(5z)³

= (3y+5z)[(3y)²–(3y)(5z)+(5z)²]

= (3y+5z)(9y²–15yz+25z²)

(ii) 64m³–343n³

The expression, 64m³–343n³can be written as (4m)³–(7n)³

64m³–343n³ =
(4m)³–(7n)³

We know that, x³–y³ = (x–y)(x²+xy+y²)

64m³–343n³ = (4m)³–(7n)³

= (4m-7n)[(4m)²+(4m)(7n)+(7n)²]

= (4m-7n)(16m²+28mn+49n²)

11. Factorise: 27x³+y³+z³–9xyz 

Solution:

The expression27x³+y³+z³–9xyz can be written as (3x)³+y³+z³–3(3x)(y)(z)

27x³+y³+z³–9xyz  = (3x)³+y³+z³–3(3x)(y)(z)

We know that, x³+y³+z³–3xyz = (x+y+z)(x²+y²+z²–xy –yz–zx)

27x³+y³+z³–9xyz  = (3x)³+y³+z³–3(3x)(y)(z)

= (3x+y+z)[(3x)²+y²+z²–3xy–yz–3xz]

= (3x+y+z)(9x²+y²+z²–3xy–yz–3xz)

12. Verify that:

x³+y³+z³–3xyz = (1/2) (x+y+z)[(x–y)²+(y–z)²+(z–x)²]

Solution:

We know that,

x³+y³+z³−3xyz = (x+y+z)(x²+y²+z²–xy–yz–xz)

⇒ x³+y³+z³–3xyz = (1/2)(x+y+z)[2(x²+y²+z²–xy–yz–xz)]

= (1/2)(x+y+z)(2x²+2y²+2z²–2xy–2yz–2xz)

= (1/2)(x+y+z)[(x²+y²−2xy)+(y²+z²–2yz)+(x²+z²–2xz)]

= (1/2)(x+y+z)[(x–y)²+(y–z)²+(z–x)²]

13. If  x+y+z = 0, show that x³+y³+z³ = 3xyz.

Solution:

We know that,

x³+y³+z³-3xyz = (x +y+z)(x²+y²+z²–xy–yz–xz)

Now, according to the question, let (x+y+z) = 0,

then, x³+y³+z³ -3xyz = (0)(x²+y²+z²–xy–yz–xz)

⇒ x³+y³+z³–3xyz = 0

⇒ x³+y³+z³ = 3xyz

Hence Proved

14. Without actually calculating the cubes, find the value of each of the following:

(i) (−12)³+(7)³+(5)³

(ii) (28)³+(−15)³+(−13)³

Solution:

(i) (−12)³+(7)³+(5)³

Let a = −12

b = 7

c = 5

We know that if x+y+z = 0, then x³+y³+z³=3xyz.

Here, −12+7+5=0

(−12)³+(7)³+(5)³ = 3xyz

= 3×-12×7×5

= -1260

(ii) (28)³+(−15)³+(−13)³

Solution:

(28)³+(−15)³+(−13)³

Let a = 28

b = −15

c = −13

We know that if x+y+z = 0, then x³+y³+z³ = 3xyz.

Here, x+y+z = 28–15–13 = 0

(28)³+(−15)³+(−13)³ = 3xyz

= 0+3(28)(−15)(−13)

= 16380

15. Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given: 

(i) Area : 25a²–35a+12

(ii) Area : 35y²+13y–12

Solution:

(i) Area : 25a²–35a+12

Using the splitting the middle term method,

We have to find a number whose sum = -35 and product =25×12=300

We get -15 and -20 as the numbers [-15+-20=-35 and -15×-20=300]

25a²–35a+12 = 25a²–15a−20a+12

= 5a(5a–3)–4(5a–3)

= (5a–4)(5a–3)

Possible expression for length  = 5a–4

Possible expression for breadth  = 5a –3

(ii) Area : 35y²+13y–12

Using the splitting the middle term method,

We have to find a number whose sum = 13 and product = 35×-12 = 420

We get -15 and 28 as the numbers [-15+28 = 13 and -15×28=420]

35y²+13y–12 = 35y²–15y+28y–12

= 5y(7y–3)+4(7y–3)

= (5y+4)(7y–3)

Possible expression for length  = (5y+4)

Possible expression for breadth  = (7y–3)

16. What are the possible expressions for the dimensions of the cuboids whose volumes are given below? 

(i) Volume : 3x²–12x

(ii) Volume : 12ky²+8ky–20k

Solution:

(i) Volume : 3x²–12x

3x²–12x can be written as 3x(x–4) by taking 3x out of both the terms.

Possible expression for length = 3

Possible expression for breadth = x

Possible expression for height = (x–4)

(ii) Volume:
12ky²+8ky–20k

12ky²+8ky–20k can be written as 4k(3y²+2y–5) by taking 4k out of both the terms.

12ky²+8ky–20k = 4k(3y²+2y–5)[Here, 3y²+2y–5 can be written as 3y²+5y–3y–5 using splitting the middle term method.]

= 4k(3y²+5y–3y–5)

= 4k[y(3y+5)–1(3y+5)]

= 4k(3y+5)(y–1)

Possible expression for length = 4k

Possible expression for breadth = (3y +5)

Possible expression for height = (y -1)

NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Summary

As this is one of the important topics in Maths, it comes under the unit – Algebra which has a weightage of 20 marks in Class 9 Maths board exams. This chapter talks about:

• Polynomials in One Variable
• Zeroes of a Polynomial
• Remainder Theorem
• Factorization of Polynomials
• Algebraic Identities

Students can refer to the NCERT Solutions for Class 9 Maths while solving exercise problems and preparing for their Class 9 Maths exams.

List of Exercises in Class 9 Maths Chapter 2:

Exercise 2.1 Solutions 5 Questions

Exercise 2.2 Solutions 4 Questions

Exercise 2.3 Solutions 3 Questions

Exercise 2.4 Solutions 5 Questions

Exercise 2.5 Solutions 16 Questions

NCERT Solutions for Class 9 Maths Chapter 2 – Polynomials

NCERT Solutions for Class 9 Maths Chapter 2 Polynomials is the second chapter of Class 9 Maths. Polynomials are introduced and discussed in detail here. The chapter discusses Polynomials and their applications. The introduction of the chapter includes whole numbers, integers, and rational numbers.

The chapter starts with the introduction of Polynomials in section 2.1 followed by two very important topics in sections 2.2 and 2.3

• Polynomials in one Variable – Discussion of Linear, Quadratic and Cubic Polynomial.
• Zeroes of a Polynomial – A zero of a polynomial need not be zero and can have more than one zero.
• Real Numbers and their Decimal Expansions – Here you study the decimal expansions of real numbers and see whether they can help in distinguishing between rationals and irrationals.

Next, it discusses the following topics:

• Representing Real Numbers on the Number Line – In this the solutions for 2 problems in Exercise 2.4.
• Operations on Real Numbers – Here you explore some of the operations like addition, subtraction, multiplication, and division on irrational numbers.
• Laws of Exponents for Real Numbers – Use these laws of exponents to solve the questions.

Key Advantages of NCERT Solutions for Class 9 Maths Chapter 2 – Polynomials

• These NCERT Solutions for Class 9 Maths helps you solve and revise the whole syllabus of Class 9.
• After going through the stepwise solutions given by our subject expert teachers, you will be able to score more marks.
• It follows NCERT guidelines which help in preparing the students accordingly.
• It contains all the important questions from the examination point of view.
• It helps in scoring well in Maths in board exams.

Frequently Asked Questions on NCERT Solutions for Class 9 Maths Chapter 2

How many exercises are present in NCERT Solutions for Class 9 Maths Chapter 2?

NCERT Solutions for Class 9 Maths Chapter 2 has 5 exercises. The topics discussed in these exercises are polynomials in one Variable, zeros of a polynomial, real numbers and their decimal expansions, representing real numbers on the number line and operations on real numbers laws of exponents for real numbers. Practice is an essential task to learn and score well in Mathematics. Hence the solutions are designed by BYJU’S experts to boost confidence among students in understanding the concepts covered in this chapter.

Why should I opt for NCERT Solutions for Class 9 Maths Chapter 2?

The concepts present in NCERT Solutions for Class 9 Maths Chapter 2 are explained in simple language, which makes it possible even for a student not proficient in Maths to understand the subject better. Solutions are prepared by a set of experts at BYJU’S with the aim of helping students boost their exam preparation.

Is NCERT Solutions for Class 9 Maths Chapter 2 difficult to learn?

No, if you practice regularly with NCERT Solutions for Class 9 Maths Chapter 2 you can achieve your goal by scoring high in finals. These solutions are formulated by a set of Maths experts at BYJU’S. Students can score good marks in the exams by solving all the questions and cross-checking the answers with the NCERT Solutions for Class 9 Maths Chapter 2.