NCERT Solutions Class 5 Maths Chapter 3-How Many Squares, is provided here for students to prepare for exams. The NCERT Solutions are prepared by experts with respect to the CBSE syllabus (2020-2021) guided by the board.
Class 5 Maths Chapter 3-How Many Squares, solved questions, helps students to draw squares from a given set of dots. With questions related to measuring sides of squares, this chapter contains a series of questions which will help them to increase their concentration on the subject. Students can download NCERT Solutions for Class 5 Maths Chapter 3 from the links given below and start practising offline.
NCERT Solutions for Class 5 Maths Chapter 3-How Many Squares:-Download PDF Here












Access Solutions for NCERT Class 5 Maths Chapter 3 How Many Squares
Page: 34
1.
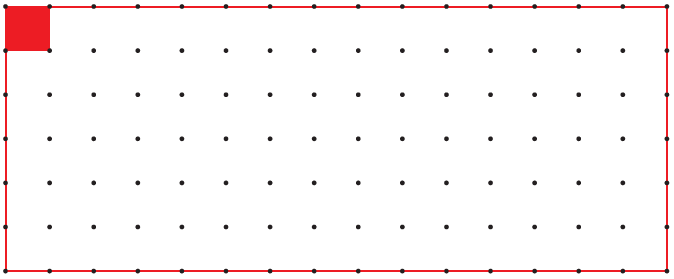
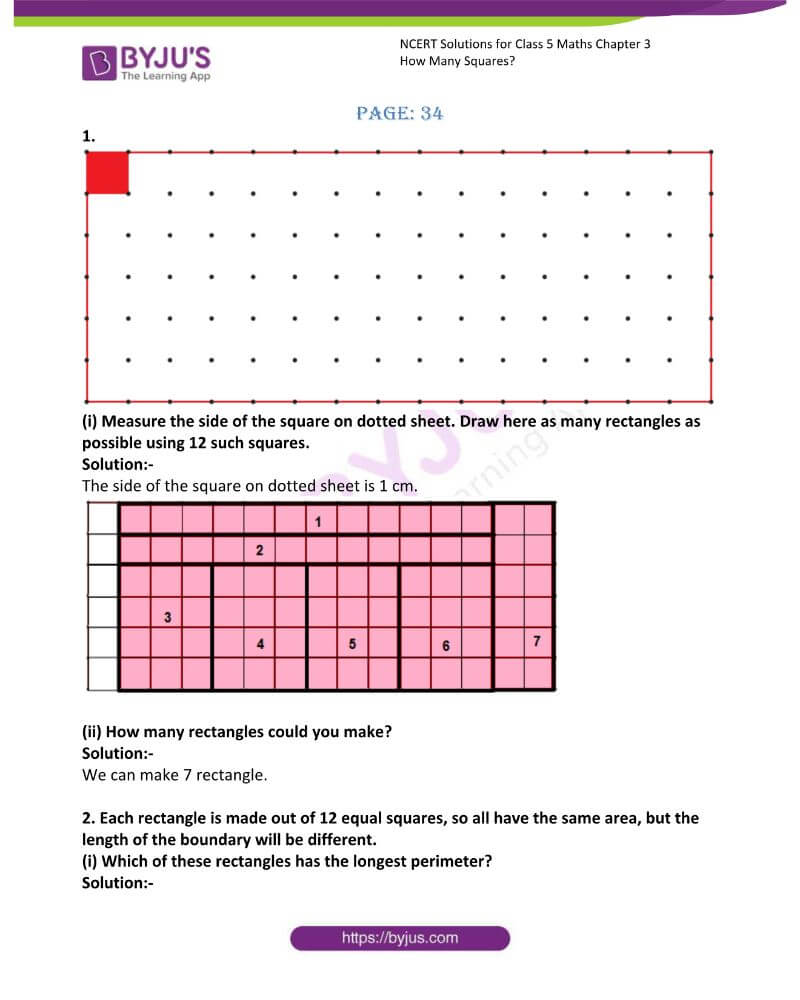
(i) Measure the side of the square on dotted sheet. Draw here as many rectangles as possible using 12 such squares.
Solution:-
The side of the square on dotted sheet is 1 cm.
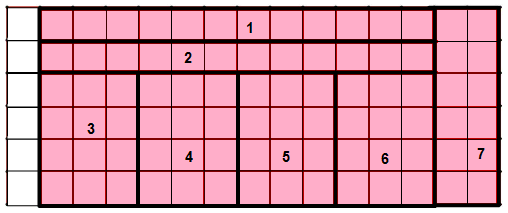
(ii) How many rectangles could you make?
Solution:-
We can make 7 rectangle.
2. Each rectangle is made out of 12 equal squares, so all have the same area, but the length of the boundary will be different.
(i) Which of these rectangles has the longest perimeter?
Solution:-
From the above figure we can say that, rectangle 1 and 2 has the longest perimeter.
We know that, perimeter of rectangle= 2 (length + breadth)
= 2 (1 + 12)
= 2 × 13
= 26 cm
(ii) Which of these rectangles has the smallest perimeter?
Solution:-
From the above figure we can say that, rectangle 3, rectangle 4, rectangle 5 and 6 rectangle has the smallest perimeter.
We know that, perimeter of rectangle= 2 (length + breadth)
= 2 (3 + 5)
= 2 × 8
= 16 cm
3.
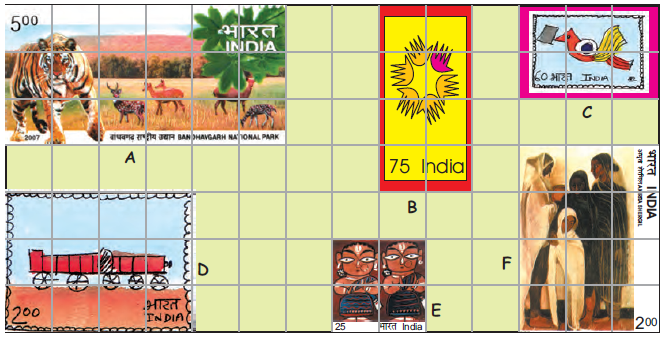
Look at these interesting stamps.
(a) How many squares of one centimetre side does stamp A cover? ________
And stamp B? ________
Solution:-
Stamp A covers 18 squares of one centimeter side, and Stamp B covers 8 squares of one centimeter side.
(b) Which stamp has the biggest area?
Solution:-
Stamp ‘A’ has biggest area, because it has 18 squares.
(i) How many squares of side 1 cm does this stamp cover?
Solution:-
This stamp has 18 squares of side 1 cm.
(ii) How much is the area of the biggest stamp?
Solution:-
The biggest stamp is in the shape of rectangle,
The area of the biggest stamp is = length × breadth
= 3 × 6
= 18 cm2
c) Which two stamps have the same area?
Solution:-
Stamp ‘D’ and stamp ‘F’ have the same area.
(i) How much is the area of each of these stamps? ____ square cm.
Solution:-
We know that, area of rectangle = length × breadth
So, Area of stamp ‘D’ = 3 × 4
= 12 cm2
Area of stamp ‘F’ = 4 × 3
= 12 cm2
Therefore area of stamp ‘D’ is equal to area of stamp ‘F’.
d) The area of the smallest stamp is _____ square cm.
Solution:-
The area of the smallest stamp is 4 square cm.
area of smallest stamp ‘E’ = length × breadth
= 2 × 2
= 4 cm2
(i) The difference between the area of the smallest and the biggest stamp is _____ square cm.
Solution:-
Area of the biggest stamp = 18 cm2
Area of the smallest stamp = 4 cm2
Then,
The difference between the area of the smallest and the biggest stamp = 18 – 4
= 14 cm2
4. Guess
a) Which has the bigger area — one of your footprints or the page of this book?
Solution:-
When comparing the area of footprints and the area of page of this book, the area of page of this book is bigger than footprints.
b) Which has the smaller area—two five-rupee notes together or a hundred rupee note?
Solution:-
A hundred rupee note has the smaller area.
c) Look at a 10 rupee-note. Is its area more than hundred square cm?
Solution:-
No, the area of 10 rupee note is not more than hundred square cm.
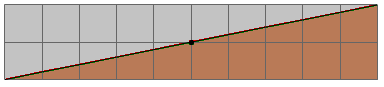
d) Is the area of the blue shape more than the area of the yellow shape? Why?
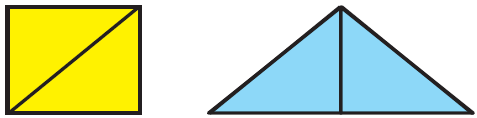
Solution:-
No, from the given image we can say that, the area of blue shape is equal to the area of yellow shape. Because, the yellow and blue shaped figures are divided into two triangles of equal areas.
e) Is the perimeter of the yellow shape more than the perimeter of the blue shape? Why?
Solution:-
No, the perimeter of the yellow shape is less than the perimeter of the blue shape. With the help of a ruler, we can able find that the length of the boundary of the blue shape is more than the length of the boundary of the yellow shape.
5. Write the area (in square cm) of the shapes below.
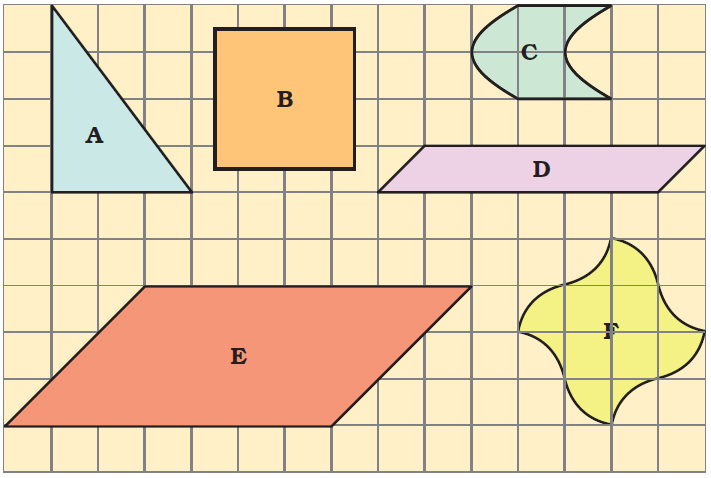
Solution:-
Area of triangle fig A = ½ × base × height
= ½ × 3 × 4
= ½ × 12
= 6 cm2
Area of square fig B = 4 complete square + 8 half squares + 4 quarter squares
= 4 + (½ × 8) + (¼ × 4)
= 4 + 4 + 1
= 9 cm2
Area of fig C = 2 complete square + 4 half square
= 2 + (½ × 4)
= 2 + 2
= 4 cm2
Area of fig D = 5 complete square + 2 half square
= 5 + (½ × 2)
= 5+ 1
= 6 cm2
Area of fig E = 18 complete square + 6 half square
= 18 + (½ × 6)
= 18 + 3
= 21 cm2
Area of fig F = 4 complete square + 4 more than half + 4 quarter square
= 4 + (¾ × 4) + (¼ × 4)
= 4 + 3 + 1
= 8 cm2
6. The blue triangle is half of the big rectangle. Area of the big rectangle is 20 square cm. So the area of the blue triangle is _______ square cm.
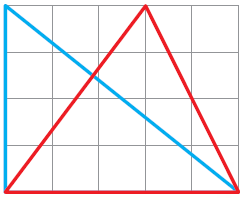
Solution:-
From the question,
Area of the big rectangle is 20cm2.
Area of the blue triangle is half of the big rectangle = 20/2
= 10 cm2
7. Ah, in it there are two halves of two different rectangles!
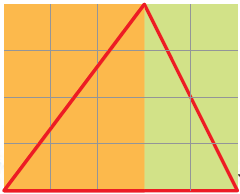
Now you find the area of the two rectangles Sadiq is talking about. What is the area of the red triangle? Explain.
From the figure, we can say that,
The orange rectangle contains 12 squares
So, area of orange rectangle = 12 cm2
Then, green rectangle contains 8 squares
So, the area of green rectangle = 8 cm2
Now, area of the orange portion of triangle = 12/2 = 6cm2
Area of the yellow portion of triangle = 8/2 = 4 cm2
Therefore, area of red triangle = 6 + 4
= 10 cm2
8. Suruchi drew two sides of a shape. She asked Asif to complete the shape with two more sides, so that its area is 10 square cm.
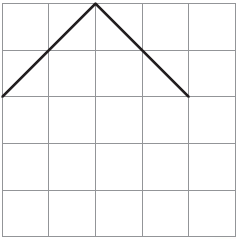
He completed the shape like this.
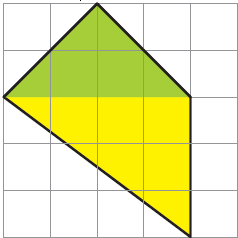
(i) Is he correct? Discuss.
Solution:-
Yes, he is correct.
(ii) Explain how the green area is 4 square cm and the yellow area is 6 square cm.
Solution:-
Green area contains = 2 complete square + 4 half square
= 2 + (½ × 4)
= 2 + 2
= 4 cm2
Yellow area contains = 3 complete square + 2 more than half + 2 half filled
= 3 + 2 + (½ × 2)
= 3 + 2 + 1
= 6 cm2
Practice time
(1) This is one of the sides of a shape. Complete the shape so that its area is 4 square cm.
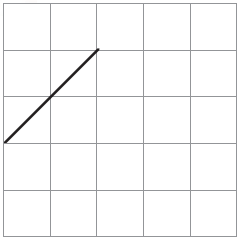
Solution:-
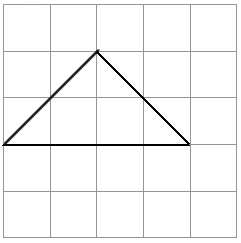
The completed shape contains = 2 complete square + 4 half square
= 2 + (½ × 4)
= 2 + 2
= 4 cm2
2. Two sides of a shape are drawn here. Complete the shape by drawing two more sides so that its area is less than 2 square cm.
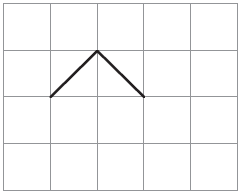
Solution:-
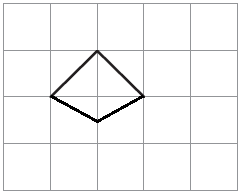
3. Here is a rectangle of area 20 square cm.
a) Draw one straight line in this rectangle to divide it into two equal triangles. What is the area of each of the triangles?
Solution:-
Area of rectangle = 10 × 2
= 20 cm2
Then, area of two equal triangles = 20/2
= 10 cm2
Because, it is given that straight line divides rectangle in to two equal triangles.
b) Draw one straight line in this rectangle to divide it into two equal rectangles. What is the area of each of the smaller rectangles?
Solution:-

Area of big rectangle = 10 cm2
The area of each of the smaller rectangle = 20/2
= 10 cm2
c) Draw two straight lines in this rectangle to divide it into one rectangle and two equal triangles.
Solution:-
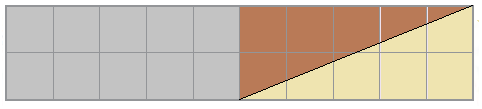
(i) What is the area of the rectangle?
Solution:-
Area of rectangle = length × breadth
= 2 × 5
= 10 cm2
(ii) What is the area of each of the triangles?
Solution:-
Area of each triangle = ½ × area of smaller rectangle
= ½ × 10
= 5 cm2
4. Puzzle with five squares
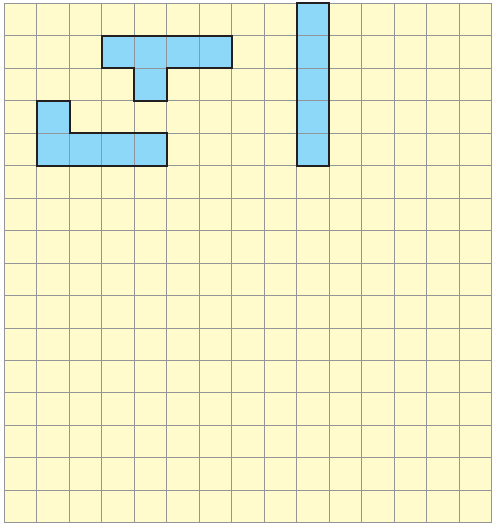
a) How many different shapes can you draw?
Solution:-
Using 5 squares, I can draw 12 shapes as show in the below,
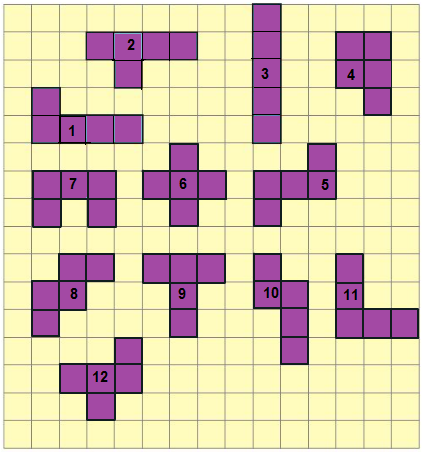
b) Which shape has the longest perimeter? How much?
Solution:-
Shape 4 has the smallest perimeter out of 12 shapes, rest of the shapes have same perimeter. i.e. = 1 + 1 + 1 + 1 + 1 + 1+ 1 + 1 + 1 + 1 + 1 + 1 = 12 cm
c) Which shape has the shortest perimeter? How much?
Solution:-
Out of 12 shapes 4 has the smallest perimeter.
i.e. = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 10 cm.
d) What is the area of the shapes? _______ square cm. That’s simple!
Solution:-
There are 12 shapes each shapes has complete five squares. Area of 1 square is equal to 1 cm2.
So, Area of each shape = 1 × 5 = 5 cm2
5. Ziri tried to make some other tiles. She started with a square of 2 cm side and made shapes like these.
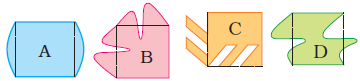
Look at these carefully and find out:
(i) Which of these shapes will tile a floor (without any gaps)? Discuss. What is the area of these shapes?
Solution:-
By observing the given figure shape C and shape D will tile a floor without any gaps.
Frequently Asked Questions on NCERT Solutions for Class 6 Maths Chapter 6
What is perimeter as explained in NCERT Solutions for Class 6 Maths Chapter 6?
In chapter 3 of NCERT Solutions for Class 6 Maths, perimeter is defined as the length of the boundary. For a rectangle, the perimeter is the sum of twice the length and twice the breadth.
What are the perimeter and area of a rectangle and a square as discussed in NCERT Solutions for Class 6 Maths Chapter 6?
The perimeter of a square = 4 x (length of a side)
The perimeter of a rectangle = 2 x (length + breadth)
And, area of a square = side x side = (side)2
Area of a rectangle = length x breadth
What are the topics covered in NCERT Solutions for Class 6 Maths Chapter 6?
The topics covered in NCERT Solutions for Class 6 Maths are drawing squares from a given set of dots, measuring sides and calculating the perimeter of squares and rectangles, finding the area of squares and rectangles by calculation and comparing the areas of different shapes/figures by counting the number of squares in it.